Apollo 11 and Fundamental Science

In July 1969, an estimated one-fifth of the earth’s population—some 3.6 billion people—watched on live television as the Apollo 11 astronauts walked on the moon. Over the years, some commentators have unkindly suggested that the only interesting spin-off from the entire enterprise was the development of moon boots. This is simply not the case. The Apollo missions made important contributions to a number of advances in fundamental science. An exquisitely precise test of the strong equivalence principle, to cite just one example, would not have been possible without scientific equipment transported to the moon during the Apollo program.

Lunar Laser Ranging

During the two and a half hours that they spent outside the moon lander, Neil Armstrong and Buzz Aldrin installed the first passive laser ranging retroreflector on the lunar surface. In November 1970, a French retroreflector was transported to the moon onboard the Soviet probe Lunokhod 1. Three further retroreflectors arrived as part of the Apollo 14, Apollo 15, and Lunokhod 2 missions.

The retroreflectors installed during these missions were substantial devices. The mirror installed during the Apollo 11 mission, for example, measured 59 × 67 × 27.5 cm. Although it had a mass of a few pounds, the retroreflector occupied a far from negligible portion of the limited space available in the Apollo Lunar Module. The fact that NASA, as part of its pioneering Apollo 11 mission, dedicated a part of the payload to fundamental physics was a magnificent gesture.

In 1962, James Faller, a graduate student at Princeton, sent a draft paper to his supervisor, Robert Dicke, entitled “A Proposed Lunar Package (A Corner Reflector on the Moon).”¹ In the top right corner of the opening page, Faller added a handwritten note: “Professor Dicke, [w]ould you see if this makes any sense.” The paper read, in part:

This note describes what is felt to be both a useful and at the same time a practical lunar package. … Recently there has been considerable discussion concerning the possibility of bouncing a laser off the moon and detecting the reflected light returning to the earth. This would permit a precise earth–moon distance measurement to be made.²

Dicke wrote his reply in the upper left corner of the opening page: “Perhaps we should discuss this.”

The idea outlined in Faller’s draft was, in effect, a lunar version of a program originally devised to measure distances to artificial satellites. Dicke, along with his colleagues William Hoffman and Robert Krotkov, had proposed the idea in a July 15, 1959 preprint, “Precision Optical Tracking of Artificial Satellites.”³

In a first approximation, lunar ranging, or the measurement of the earth–moon distance as a function of time, is straightforward. A strong ultrashort laser pulse is directed to a retroreflector on the lunar surface, where it arrives with an aperture of approximately 6.5 kilometers.⁴ These mirrors are termed retroreflectors because the light bounces back in the direction from which it originated, rather than the complementary one. About 1/10¹⁷ of the monochromatic photons emitted make it back and may be detected. The quasi-instantaneous distance from the laser emitter to the reflector can be obtained by multiplying half the time spent on the round trip by the velocity of light, c. After several decades of sporadic measurements made using this method, the distance from the earth to the moon has been established with an uncertainty of less than one centimeter. Another useful result from these experiments was the discovery that the moon recedes from the earth by about 3.8 cm each year, due to tidal friction.

The Nordtvedt Test

In the late sixteenth century, Galileo Galilei supposedly dropped two spheres of different masses from the Leaning Tower of Pisa in order to prove that objects fall at the same speed regardless of their masses. In 1968, Kenneth Nordtvedt proposed an experiment, now known as the Nordtvedt test, to examine the same problem on much larger scale: the question of whether the earth and the moon fall toward the sun at the same rate.⁵ Nordtvedt’s key insight concerned the role played by the gravitational self-masses of the two lighter bodies.

If the earth and moon fall toward the sun at different rates of acceleration, the moon’s orbit is polarized, or stretched, in the direction of the sun.⁶ The effect is maximal when the earth, moon, and sun are aligned. For any other synodic angle—that is, the angle between the direction of the moon and sun as seen from the earth—the effect varies in a sinusoidal manner. The hypothetical radial modification of the moon’s orbit would then be proportional to the difference in accelerations multiplied by the cosine of (2πt/T), where T is the synodic period of the successive alignments of the three bodies.⁷ Calculating the coefficient of proportionality is less straightforward.⁸ Having a specific period or frequency is a welcome feature in the search for a hypothetical effect. Indeed, a fair proportion of high-precision physics would cease to exist in the absence of Jean-Baptiste Joseph Fourier’s teachings. In this case how to transform information from positions in space to frequencies.

The mass of an atom, say hydrogen, is the sum of the masses of its electron, proton, and the negative contribution due to the electromagnetic binding between the two charged constituents. A binding energy, ΔE, corresponds to a contribution to the mass of ΔE/c². The cited mass could be inertial, as is the case for m in E = mv²/2, where E is the nonrelativistic kinetic energy. Or, it could be gravitational, as is the case for m in F = GmM/R², where G is Newton’s constant, F is the weight of the object, M is the earth’s mass, and R is the earth’s radius. The assumption that these two logically-independent roles played by m are physically equal is known as the weak equivalence principle. A precise test of this principle involves comparing the inertial and gravitational masses for substances which have the same constituents—electrons, protons, and neutrons—but differ in terms of their atomic, molecular, and crystal binding energies.⁹

Two objects with different ratios of gravitational to inertial mass would fall with a difference in acceleration, Δg. Some recent limits from laboratory and satellite experiments,¹⁰ normalized to the (almost) common g, are:

Δg[Be, Ti]/g < (0.3 ± 1.8) × 10^–13;

Δg[Be, Al]/g < (–0.7 ± 1.3) × 10^–13; and

Δg[Be, Pt]/g < (–1 ± 9[stat] ± 9[syst]) × 10^–15.

These limits to departures from the weak equivalence principle are extremely impressive.

Tests of the strong equivalence principle have been deduced from lunar ranging data. If the radial distance of a volume element of an object from its center is r and its local density is ρ, the energy of the gravitational attraction between any two volume elements is

$\Delta {\mathrm{E}}_{\mathrm{G}}=-\int \frac{\mathrm{G}\rho \left(\overrightarrow{r}\right)\rho \left(\overrightarrow{r}\text{'}\right)}{2\left|\overrightarrow{r}-\overrightarrow{r}\text{'}\right|}{d}^{3}r{d}^{3}r\text{'}$,¹¹

and it ought to contribute to the rest mass of the object an amount ΔM = ΔE_G/c². If an object’s mass, without this contribution, is defined as M₀, the strong equivalence principle states that the pull of gravity acts on M = M₀ + ΔM. In effect, the weight of gravity is added to the weak equivalence principle, stating that gravitational self-energies also gravitate. The strong principle is respected by general relativity, while alternative theories of gravity allow for M = M₀ + ηΔM, with η ≠ 1.¹²

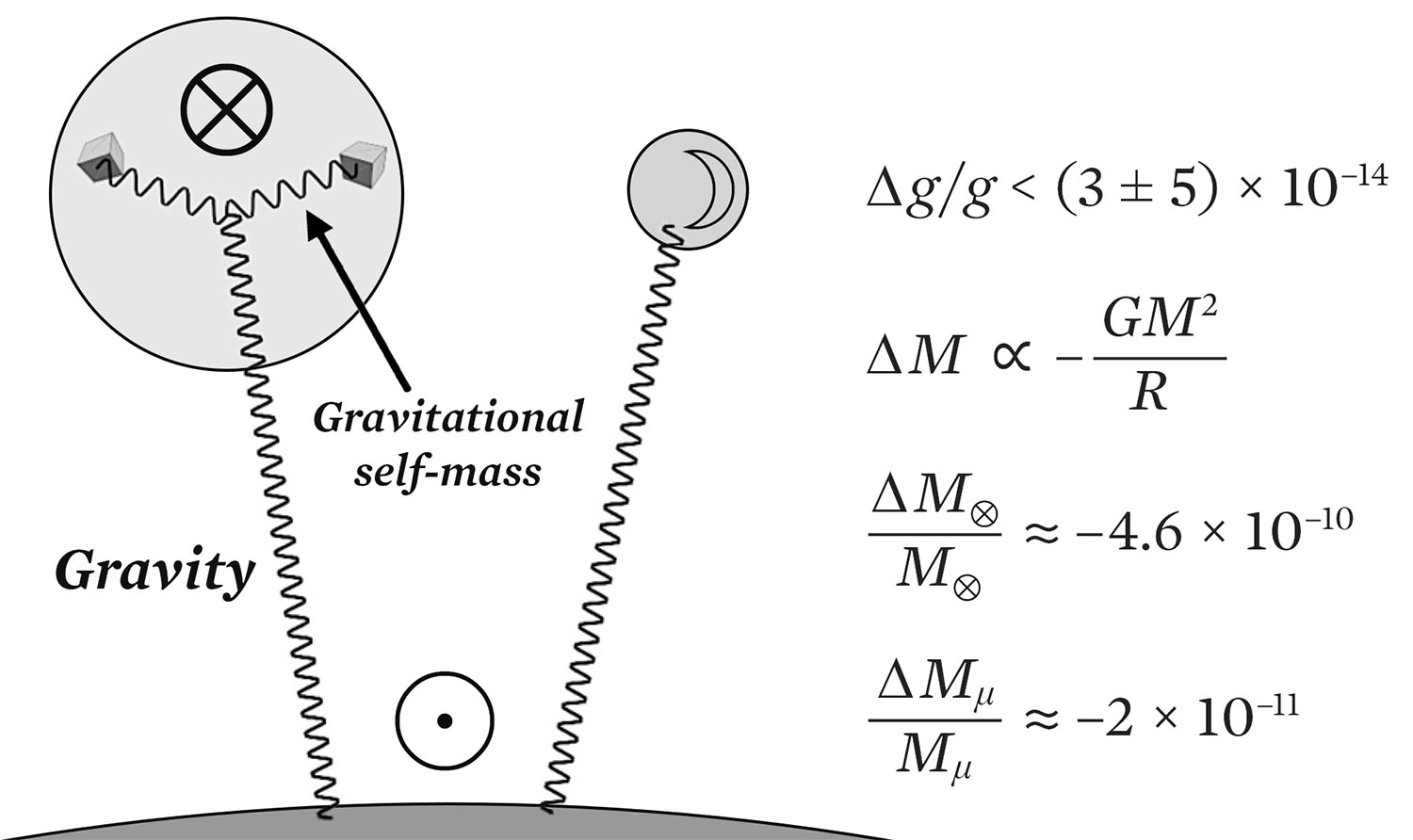
In an atom, the gravitational binding energy is negligible. Gravitational forces—with the exception of the cosmological constant¹³—always have the same sign and increase linearly with mass. The earth and moon are sufficiently large that their gravitational self-masses are not entirely negligible. The ratios of the gravitational self-mass to the total mass for the earth and moon are approximately –4.64 × 10^–10 and –2.0 × 10^–11, respectively, as shown in Figure 1.

The lunar-ranging observations constrain the equality of the accelerations with which the moon and the earth fall toward the sun to the level

Δg[E, M]/g < (3 ± 5) × 10^–14.

Given the estimated gravitational self-masses of the earth and moon, the non-observation of a synodic Nordtvedt polarization of the moon’s orbit results in a value, or the corresponding upper limit, of the strong-equivalence-violating parameter Δη ≡ η – 1:¹⁴

Δη = (–0.2 ± 1.1) × 10^–4.

This is the precision to which lunar ranging reveals that, as in Albert Einstein’s theory, gravity gravitates. As shown in Figure 1, the gravitational self-masses of the earth and the moon—represented by the wiggly lines between two volume elements—are pulled by the sun’s gravity just as much as the bulk of their masses are.

Even if individual gravitons have not been detected—a situation that seems unlikely to change in the foreseeable future—a particle theorist would be tempted to interpret the vertex of the wavy lines in Figure 1 as the triple-graviton coupling.¹⁵ A fundamental difference between electrodynamics and gravity is that the latter is nonlinear—the carriers of the force, unlike photons, also act as sources of gravity. Another way to state that gravity gravitates is that general relativity is a non-abelian gauge theory. The same statement applies to the electroweak Standard Model of quarks and leptons.

Quantum chromodynamics (QCD), the theory that describes the strong interactions of quarks and gluons, is entirely akin to general relativity in the sense that gluons have color charges and couple to other gluons. In spite of the fact that gravity is the weakest and QCD is the strongest of the known forces between elementary particles at accessible energies, the triple-graviton coupling is measured with three orders of magnitude more precision than that of the triple-gluon coupling. Testing QCD to an astronomically equivalent level of accuracy would be no mean feat.

There is an unlikely loophole in the Nordtvedt test. The different chemical mass compositions of the earth and the moon could be said to conspire—via unknown feeble composition-dependent forces—to invalidate the conclusion that the strong equivalence principle is tested to the stated precision. To distinguish weak from strong equivalence-principle effects, the Eöt-Wash group at the University of Washington performed a torsion-balance experiment using test masses of similar composition to the earth and moon.¹⁶ Combining torsion-balance results with the latest lunar-ranging analyses yielded the result¹⁷

Δη = (4.4 ± 4.5) × 10^–4.

This result is only slightly less restrictive than the nonconspiratorial one.

The effects discussed thus far are not the only ones needed to conduct a test of general relativity. In addition to orbital effects, the data analysis requires, among many others, corrections due to geophysical and rotational effects for the earth and the moon. Lunar ranging can also be used to conduct other tests, such as a hypothetical variation with time of Newton’s constant.¹⁸ The following are recent results:

Ġ/G = (6 ± 7) × 10^–13/year;¹⁹

Ġ/G = (2 ± 7) × 10^–13/year; and

$\ddot{\mathrm{G}}$/G = (4 ± 5) × 10^–15/year².²⁰

These limits imply a variation in G of less than one percent over the age of the universe.²¹

As part of their mission, the Apollo 11 astronauts also set up a seismometer on the lunar surface. Although not as significant for fundamental science as the experiments conducted using the retroreflectors, a number of discoveries were made using this device and other similar ones. Mostly generated by meteorite impacts, so-called moonquakes allowed researchers to study the moon’s internal structure. It turns out that the moon, not unlike the earth, has an iron core. Interesting findings also emerged from even less likely sources. Consider the iconic photograph of Aldrin’s footprint on the lunar surface. This image revealed much about the moon’s soil, including its fine-grained nature and cohesiveness.

Not for All of Mankind

In contrast to the lunar ranging experiments, other aspects of the Apollo program provoked varying degrees of controversy. On Christmas Eve 1968, the Apollo 8 astronauts—Frank Borman, Jim Lovell, and Bill Anders—took the famous photograph now known as Earthrise while in orbit around the moon. They also read aloud a passage from the Old Testament. An atheist activist, Madalyn Murray O’Hair, subsequently sued NASA, asserting that her First Amendment rights had been violated. O’Hair had previously been involved in a successful Supreme Court case that led to a ban on mandatory prayer and Bible readings in US public schools. The judge hearing the Apollo 8 case dismissed the lawsuit, and the Supreme Court declined to hear it due to lack of jurisdiction.

The act of raising the US flag on the moon was even more contentious. It was felt by some that planting a flag gave the impression that the US was taking possession of the moon, a clear violation of the Outer Space Treaty.²² In 1969, NASA’s appropriation bill stated that for any mission funded entirely by the US government, no flag other than the US flag could be placed on the surface of the moon or any planet. The authors of the bill were careful to note that this act was “intended as a symbolic gesture of national pride in achievement and is not to be construed as a declaration of national appropriation by claim of sovereignty.”²³ In the end, it was decided that a US flag would still be raised, but a plaque would also be placed in close proximity emphasizing that the astronauts “came in peace for all mankind.”

Some of the experiments performed during the Apollo missions were less than strictly scientific in nature.²⁴ During his voyage to the moon onboard Apollo 14, the astronaut Edgar Mitchell performed an unauthorized ESP (extrasensory perception) experiment. On four occasions during the journey, Mitchell attempted to transmit a series of symbols to a team of psychics back on Earth using ESP. Prior to each transmission, Mitchell generated groups of twenty-five random numbers using only the digits 1 to 5. Each number was assigned one of the five Zener symbols often used during ESP tests. Mitchell would then think about each symbol for fifteen seconds before moving on to the next.²⁵ The psychics reportedly guessed the right symbols fifty-one times out of 200, a success rate that Mitchell later described as “far exceeding anything expected.”²⁶ The experiment had been designed to take place at prearranged times, but various problems and delays meant that Mitchell was always running behind schedule. Rather than admit the timing mishap, in his paper for the Journal of Parapsychology, he simply changed the goal of the experiment to a study of precognition.²⁷

The Apollo Legacy

There is plenty of evidence to counter the allegation that nothing of any lasting use, especially in technological terms, emerged from the Apollo program. On its website, NASA provides a long list of benefits and developments,²⁸ including

• cooling suits and flame-resistant materials, now used by racing drivers, nuclear reactor technicians, and others;
• chemical processes for toxic waste removal in recycled fluids, now used in kidney dialysis;
• water purification technology currently used in some community water supply systems;
• physical therapy and athletic development machines developed from a space cardiovascular conditioner;
• common home insulation, built after the insulating barriers made of metalized foil laid over a core of propylene or mylar, which protected astronauts and the delicate instruments of their spacecrafts from radiation and heat;
• freeze-dried foods that preserve nutrients;
• an environmentally friendly building material, Teflon-coated fiberglass, evolved from the same fabric used in Apollo-era spacesuits;
• retroreflectors similar to the lunar-ranging mirrors, used to detect hazardous gases; and
• dry lubricant coatings, developed to avoid the outgassing of lightweight metals that would result in the malfunctioning of lubricants, now employed in laser manufacturing and pizza making.

Current estimates of the Apollo program’s total cost vary considerably. Forbes and the BBC have reported figures adjusted for inflation of 152 billion and 175 billion dollars, respectively.²⁹ Given the scale of the investment, more technological spin-offs might perhaps have been expected. The value of the Nordtvedt test cannot be stated in monetary terms, but other areas of research, such as condensed matter and particle physics, have had a much larger spinoff-to-cost ratio.

On May 25, 1961, as part of an address to Congress and the nation, President John F. Kennedy remarked:

I believe that this nation should commit itself to achieving the goal, before this decade is out, of landing a man on the Moon and returning him safely to Earth. No single space project … will be impressive to mankind, or more important … and none will be so difficult or expensive to accomplish.³⁰