Categories: From Zero to Infinity

Schapira, Pierre

This essay revisits and develops ideas presented at a conference dedicated to Gilles Châtelet and in various seminars. Gilles was a singular personality, both a mathematician and a philosopher, and I do not think I betray his memory in writing that he was also a friend.¹ This essay is written for people like Gilles, open to new languages and new ideas—needless to say, not so many people, and not especially mathematicians.

The following opening remarks are mostly a pretext to illustrate the thesis that mathematical concepts do not differ fundamentally from philosophical concepts, nor from the ideas of everyday life. Of course, this is not to suggest that mathematics and ordinary intuition are always in harmony; it is often the contrary, as one can see with, for example, the notion of infinity.²

Any student who attempts to solve an equation or a system of equations is confronted by two problems. Does a solution exist? And, if so, is it unique? In set theory, the existence of a solution is reflected in its belonging. A solution does not exist in the abstract; it either belongs to a set, or does not. In mathematics there is nothing to prevent one from conceiving an object that does not exist. The real questions then become: is the created object of interest? And what is its geometric meaning? To solve an equation that has no solution in a given set, one can add a formal solution to that set. Generally, this process is of absolutely no interest, but it is not always the case. Adding the root of $- 1$ to the real numbers in order to solve the equation $x^{2} = - 1$ is certainly not without interest since it allows us to find solutions for all polynomial equations.

But existence is not the theme of this paper. For some psychological reason, existence is privileged over uniqueness; intuitively, one tends to consider it more important. Yet in reality, uniqueness precedes existence, to paraphrase a well-known philosopher;³ it comes before, and this “before” has a precise meaning. In practice, also, uniqueness is often easier to prove than existence.⁴

Here I will consider uniqueness, or, rather, the concept of identity, and how it functions.⁵ I will therefore address the status of equality in mathematics and its variants, namely isomorphism, equivalence, and so on. This issue has until recently been totally ignored, but is of such importance that it may potentially lead us to question set theory itself.

To conclude these introductory remarks, an observation. Authors writing about mathematics for a readership beyond academic circles are faced with the predicament of an audience that possesses, at best, a very limited understanding of the true nature of mathematics, yet is seemingly allergic or, at worst, openly hostile to anything remotely connected with the field.⁶ This is changing. Slowly. Recently, a number of books has been published that attempt to make mathematics—or perhaps, in some cases, the author—more accessible to the public.⁷ One such book, Eloges des mathématiques (In Praise of Mathematics) by Alain Badiou, is perhaps worth noting. But, if Badiou defends the idea that mathematics is an integral part of culture, and especially of philosophical culture, it is only to better place mathematics at the service of highly questionable philosophical–political ideas.⁸

Sets and Functions/Categories and Functors

Among the educated, mathematics is often associated, if not identified, with the set theory that emerged in the second half of the nineteenth century from the work of Georg Cantor. Modern mathematics is developed within the framework of this theory, in the axiomatic of Zermelo–Fraenkel (or ZFC, C for the axiom of choice).

Over the past fifty years or so, this theoretical point of view has been supplanted in many fields of mathematics and physics by the category theory introduced by Samuel Eilenberg and Saunders Mac Lane and developed superbly by Alexander Grothendieck.⁹ The underlying idea of category theory is that the power of mathematical objects is only fully realized when they are placed in relation with other objects of the same type. This can be seen as part of a broad intellectual movement that emerged during the 1950s, of which the structuralism of Claude Lévi-Strauss and the linguistics of Noam Chomsky are also examples. The move from sets to categories can therefore claim the status of a conceptual revolution.

Yet, just as the theory of relativity is not a substitute for classical mechanics, the theory of categories is not a replacement for set theory. Instead, it enriches it. In practice, for example, the language of categories tends to use the axiomatic of sets.

A set $A$ is a collection of elements $a, b, c ...$ with no relations between them, such as the points of a geometric space. One says that $a$ belongs to $A$ and writes $a \in A$ . The only relations between $a$ and $b$ are the equality $a = b$ or its negation $a \neq b$ .

Given two sets $A$ and $B$ , a map (also called a function) $φ : A \to B$ associates to any element $a \in A$ a unique element $φ (a) \in B$ . Given a map $φ : A \to B$ and a map $ψ : B \to C$ , we can define a new map $ψ \circ φ : A \to C$ by setting $(ψ \circ φ) (x) = ψ (φ (x))$ . The family of all sets is the first example of a category. The category Set has sets for objects, and, given two sets $A$ and $B$ , the morphisms from $A$ to $B$ are the maps from $A$ to $B$ . Axiomatizing the properties of these maps produces the concept of a category.

As a set possesses elements, a category 𝒞 possesses objects $X, Y, Z, ...$ but now, given two objects $X$ and $Y$ in 𝒞, one has a set Hom_𝒞 $(X, Y)$ , called the set of morphisms from $X$ to $Y$ . An element $f$ of Hom_𝒞 $(X, Y)$ is represented by an arrow $f : X \to Y$ or $X \overset{f}{\to} Y$ . It is then said that $X$ is the source of $f$ , and $Y$ its target. Warning: the objects $X$ , $Y$ , etc. are not sets in general and, a fortiori, a morphism is not necessarily a map of sets. Morphism is a name given to the elements of the set Hom_𝒞 $(X, Y)$ , nothing more.

If $g : Y \to Z$ is another morphism whose source is the target of $f$ , one can compose (it is an axiom, not a property) $g$ and $f$ as a morphism $g \circ f : X \to Z$ :

,

and one assumes that composition is associative: for arrows $X \overset{f}{\to} Y \overset{g}{\to} Z \overset{h}{\to} W$ one has

$h \circ (g \circ f) = (h \circ g) \circ f$

visualized by a commutative diagram

.

Therefore, the two methods for going from $X$ to $W$ —one passing through $Y$ and the other passing through $Z$ —give the same result. The commutativity of the diagram reflects the axiom of associativity of the morphisms.

Finally, for each object $X$ there is an arrow ${id}_{X} : X \to X$ which functions as an identity map and which satisfies $f \circ {id}_{X} = f$ for any $f : X \to Y$ and ${id}_{X} \circ g = g$ for any $g : Z \to X$ .

The first example of a category is thus the category Set, of sets whose objects are the sets and where the morphisms are the maps between sets. But the set of all sets is not a set; Bertrand Russell showed that there exists no set of all sets, a variant of the Greek paradox, “All Cretans are liars.”

To escape from this paradox, one works in a given universe 𝒰 and gets the category 𝒰-Set of sets belonging to the universe 𝒰.¹⁰ What is a universe? It is a very big set, containing the set $Z$ of natural integers, and is stable under a range of operations.

Any user of categories quickly faces inextricable problems if they do not use the concept of a universe, or other equivalent notions such as that of the inaccessible cardinal. But, do universes exist? The theory of universes was introduced in an appendix to a paper by Grothendieck and Jean-Louis Verdier, “Théorie des topos et cohomologie étale des schemas.”¹¹ It also presented the fundamental axiom that any set belongs to some universe. Although signed “N. Bourbaki,” the style and objective of the appendix are at odds with what we are accustomed to from the Bourbaki group in this period. It would be interesting to know the exact role played by Grothendieck in the development of this text. The Bourbaki group, it should be noted, has published almost nothing during the last forty years. Grothendieck withdrew from the group in the early 1960s.

A very natural and intuitive category is the category Set^f of finite sets. Much of primary school mathematics is devoted to it, or should be.

Undergraduate students in mathematics usually encounter two categories. The first is the category ${Vect}^{f} (R)$ whose objects are finite dimensional vector spaces over the field $R$ of real numbers (or better, the field $C$ of complex numbers); here the morphisms are the linear maps. The second is the category Top whose objects are topological spaces, those on which there is a notion of neighborhood or limit. Here the morphisms are the continuous maps, namely, maps which respect limits.

For a category 𝒞 one gets a new category 𝒞^op, the opposite category, by keeping the same objects but reversing the arrows. A morphism $f : X \to Y$ in 𝒞^op is by definition nothing but a morphism $g : Y \to X$ in 𝒞.

The fundamental premise of category theory is that, beyond contemplating these objects, we must look at the relations among them, that is, their morphisms. What then is a morphism of categories? This is called a functor. Given two categories 𝒞 and 𝒞', a functor $F :$ 𝒞 →𝒞' sends any object $X$ of 𝒞 to an object $F (X)$ of 𝒞' and any morphism $f : X \to Y$ to a morphism $F (f) : F (X) \to F (Y)$ , with the obvious conditions that $F$ commutes with the identities: $F ({id}_{X}) = {id}_{F (X)}$ and with the compositions $F (g \circ f) = F (g) \circ F (f)$ . One can easily compose functors and derive the category 𝒰-Cat, living in a bigger universe. To remain in the universe 𝒰, one must restrict oneself to small categories, giving the 𝒰-category small-Cats.

The category Set has beneficial properties for other categories. Given a category 𝒞, it is possible to embed it in a larger category which will have, more or less, the same properties as Set. This is the category 𝒞^ of presheaves on 𝒞, namely, the category of functors from 𝒞^op to Set. For that purpose, to any $X \in$ 𝒞, one associates the presheaf which, to any object $Y$ of 𝒞, associates the set Hom_𝒞 $(Y, X)$ . That this functor from 𝒞 to 𝒞^ keeps the properties of 𝒞 (one says that this functor is fully faithful) is the famous Yoneda lemma.

One of the major traps of the category Set is that it is not equivalent to its opposite category. Set theory is not symmetric, and this lack of symmetry is the source of many errors among students.

Let me now give a proof, one that is primarily of interest for those who have some mathematical background, without being experts.

The empty set $\emptyset$ is an initial object in the category Set, meaning that for any set $X$ , there exists one, and only one, map from $\emptyset$ to $X$ . Similarly, a set reduced to a single element, say pt, is terminal, meaning that for any set $X$ , there exists one, and only one, map from $X$ to pt. Assume that there exists a functor $F :$ Set → Set^op which is an equivalence of categories (putting aside the exact definition and for the moment leaving it to the reader’s intuition). Then $F (pt) = \emptyset$ and $F (\emptyset) ≃ pt$ .¹² We deduce

${Hom}_{Set} (pt, X) ≃ {Hom}_{{Set}^{op}} (F (pt), F (X))$

$≃ {Hom}_{Set} (F (X), F (pt)) ≃ {Hom}_{Set} (F (X), \emptyset)$ .

If one chooses for $X$ a set with two elements, then ${Hom}_{Set} (pt, X)$ has two elements, as opposed to ${Hom}_{Set} (F (X), \emptyset)$ which has one element if $F (X)$ is empty (the identity of the empty set), and no element otherwise.

Equality and Isomorphisms

In a set $A$ we have the notion of equality. Given $a$ and $b$ , either they are equal or unequal. Category theory is powerful because it has a much richer concept than that of equality, namely, that of isomorphism. One says that $f : X \to Y$ is an isomorphism if there exists $g : Y \to X$ such that the composition $g \circ f$ is ${id}_{X}$ and the composition $f \circ g$ is ${id}_{Y}$ : . If there exists an isomorphism between $X$ and $Y$ , one writes $X ≃ Y$ . Two isomorphic objects in a category will then share the same properties, without being identical.

A map $f$ between two finite sets $A$ and $B$ is injective if for any $a_{1} \neq a_{2}$ one has $f (a_{1}) \neq f (a_{2})$ . It is surjective if, for any $b$ in $B$ , there exists $a$ in $A$ with $f (a) = b$ . If it is both injective and surjective, a map is bijective.

It is easily proven that a map $f$ from $A$ to $B$ is an isomorphism if and only if it is bijective, and two finite sets are isomorphic (as sets) if and only if they have the same number of elements. For example, the sets $A = {a, b, c}$ and $B = {d, e, f}$ are isomorphic. Note that there are several, exactly six, isomorphisms from $A$ to $B$ , two of which are as follows:

.

The concept of an integer emerges; it is what remains after identifying isomorphic finite sets. It is nothing but a finite set, up to isomorphism.

The set $N$ of non-negative integers is the decategorification—ignoring the morphisms and instead identifying isomorphic objects—of the category Set^f of finite sets.

The intervals $X = [0,1]$ and $Y = [0,2]$ of the real line $R$ are isomorphic in the category Top of topological spaces. The continuous map $f : X \to Y$ , $x \mapsto 2 x$ has for inverse the map $g : Y \to X$ , $y \mapsto y / 2$ . Similarly, if a little more complicated, the real line $R$ is topologically isomorphic to the open interval $(0,1)$ .

On the other hand, the real plane $R^{2}$ is isomorphic to the real line $R$ as a set, not as a topological space. This is not an obvious result.

2-categories and 2-isomorphisms

Categories, in a given universe 𝒰, and the functors between categories define a new category, the category 𝒰-Cat. But there also exists a natural notion of morphisms of functors. For two functors:

$F, G :$ 𝒞 ⇉ 𝒞',

a morphism $θ : F \to G$ is the data for any $X \in$ 𝒞 of a morphism $θ_{X} : F (X) \to G (X)$ such that for any morphism $f : X \to Y$ in 𝒞, the diagram below commutes:

.

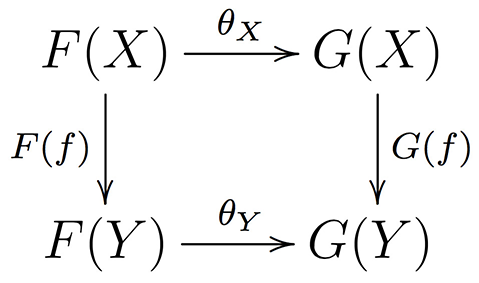This shows that the category 𝒰-Cat is not just a category, it is a 2-category. Roughly speaking, a (strict) 2-category 𝒞 is a category (a 1-category) such that for any pair of objects $X, Y$ of 𝒞, the set Hom_𝒞 $(X, Y)$ is the set of objects of a category. For any pair of objects of Hom_𝒞 $(X, Y)$ , that is, for any pair of morphisms f, g : X ⇉ Y, one has a set of morphisms from $f$ to $g$ . Such a morphism of morphisms is visualized as follows:

.

It is thus natural to think of objects of categories as being 0-dimensional, morphisms as being 1-dimensional, and 2-morphisms as being 2-dimensional. Or one can think of sets as being 0-dimensional objects, or sets of points without relations, categories as being 1-dimensional objects, or points and arrows between two points, and 2-categories as being 2-dimensional objects. One can then imagine various $n$ -categories for $n \geq 2$ , a 0-category being a set and a 1-category a usual category.

Recall that in a category 𝒞 a morphism $f : X \to Y$ is an isomorphism if there exists $g : Y \to X$ such that $g \circ f = {id}_{X}$ and $f \circ g = {id}_{Y}$ . In a 2-category, one then has a weaker notion. One requires $g \circ f$ to be isomorphic to ${id}_{X}$ in the category Hom_𝒞 $(X, X)$ and $f \circ g$ to be isomorphic to ${id}_{Y}$ in the category Hom_𝒞 $(Y, Y)$ . Then, one says that $X$ and $Y$ are equivalent or 2-isomorphic. The old isomorphisms become 1-isomorphisms and the equalities become the 0-isomorphisms.

In an $n$ -category, there are thus $n + 1$ levels of isomorphisms, with 0-isomorphic meaning equal.

If two categories 𝒞 and 𝒞' are equivalent, i.e. 2-isomorphic in the 2-category 𝒰-Cat, then it is possible to translate the properties of 𝒞 into the formalism of 𝒞'. This process has sometimes spurred spectacular discoveries.

Among mathematicians, a popular pastime is finding equivalent categories which, at first glance, are extremely different. Mirror symmetry, which emerges from physics and, in particular, from string theory, is, in the formalism of Maxim Kontsevich, an equivalence of categories.

A basic example of equivalence of categories is as follows. Consider on one side the category ${Vect}^{f} (R)$ of finite-dimensional vector spaces over the field $R$ of real numbers and, on the other side, the category 𝒜 whose objects are the integers $N = {0,1,2, ...}$ and the morphisms from $m \in N$ to $n \in N$ , the matrices $(n, m)$ with coefficients in $R$ . There exists a natural functor from 𝒜 to ${Vect}^{f} (R)$ which associates the space $R^{n}$ to the integer $n$ and which associates to a matrix $(n, m)$ a certain linear map from $R^{m}$ to $R^{n}$ . Much of a typical undergraduate algebra course is devoted to showing that this construction is functorial and that the obtained functor is an equivalence of categories.

From Local to Global: Gluing and Torsion

Mathematicians love to glue objects in a local context, switch to a global perspective, and, if the objects cannot be glued globally, calculate the obstructions which prevent it. Here the problem of the status of isomorphisms becomes fully relevant. These obstructions sometimes have a physical interpretation. A problem that at first glance appears to be purely theoretical is revealed to be, in fact, concrete.

A few examples follow.

The sphere $S^{2}$ is locally isomorphic—in the topological meaning—to the plane. In the case of the spherical earth, this isomorphism allows for the production of road maps. But no one has made a road map of the earth in its entirety. This is not by chance. They cannot be made. A topological obstruction prevents global isomorphisms between the sphere and the plane. But, forgetting the topology, as sets this obstruction disappears.

Consider a Moebius strip $X$ cut into three pieces $X_{1}$ , $X_{2}$ , and $X_{3}$ such that there are no 3-by-3 intersections.¹³

One can consider each $X_{i} (i = 1,2,3)$ as the copy of a rectangle $X_{0}$ . The Moebius strip is then obtained by gluing $X_{1}$ and $X_{2}$ , then $X_{2}$ and $X_{3}$ , and finally $- X_{3}$ and $X_{1}$ where $- X_{3}$ denotes the rectangle deduced from $X_{3}$ by exchanging up and down.

Now let us give $X_{0}$ an oriented angle $F_{0}$ . The rectangle $- X_{0}$ now has the oriented angle $- F_{0}$ . Consider three copies $(X_{1}, F_{1})$ , $(X_{2}, F_{2})$ , $(X_{3}, F_{3})$ of $(X_{0}, F_{0})$ . One glues $(X_{1}, F_{1})$ and $(X_{2}, F_{2})$ , then $(X_{2}, F_{2})$ and $(X_{3}, F_{3})$ , but one cannot glue $(X_{1}, F_{1})$ with $(- X_{3}, - F_{3})$ .

This example shows that the concept of isomorphism is essential for the gluing process; only isomorphic objects can be glued. This holds true in the category we are working in, in this case the oriented open subsets of the plane.

The notion of an oriented angle has no meaning on a Moebius strip. If we place such an angle on the strip and move it, after one turn it becomes the opposite angle! And of course, after two turns, the initial angle reappears. In this case, oriented angles, despite being locally perfectly defined, do not exist globally. The Moebius strip is not orientable.

Figure 1: The Moebius strip

The example of the Moebius strip is not exceptional or pathological. On the contrary, it is a prototype of situations encountered every day in mathematics. Although these oriented angles cannot be glued together, they belong to a globally well-defined mathematical object, the orientation sheaf.

Weak 2-categories and ∞-categories

In a usual category, a 1-category, the composition of morphisms is associative. If $f, g, h$ are composable morphisms, then $(h \circ g) \circ f = h \circ (g \circ f)$ . But when working in a 2-category, the morphisms $f, g, h$ no longer belong to sets but to categories, and as we have seen, the notion of equality can be weakened by that of isomorphism. We then obtain the concept of a weak 2-category in which composition is only associative up to isomorphism.

One can iterate these constructions and obtain the so-called ∞-categories. An example is the open subset Ω of the plane $R^{2}$ . The objects are the points of Ω, the morphisms $f : x \to y$ are the continuous paths going from $x$ to $y$ , and the 2-morphisms are the homotopies of such paths, that is, the continuous deformations of the paths, etc. Composition of paths is associative and unital, but only up to homotopy. One can compose these homotopies up to homotopy, and so forth.

This example is emblematic of an ∞-groupoid; at each order the morphisms are isomorphic up to homotopy. If this property is only satisfied at order $\geq 1$ , one gets the notion of (∞, 1)-category. As a result of the work of Jacob Lurie and Bertrand Toën in particular, this theory is currently replacing classical theory.¹⁴

Towards the Revolution

The idea that the properties are satisfied only up to homotopy is close to attaining ascendancy in mathematical logic. Vladimir Voevodsky has initiated a project to replace existing set theory ZFC with a new theory in which, for the concept of equality, we would substitute that of equality up to homotopy. This is the univalency axiom.¹⁵ In this new setting, the ∞-categories would become the usual categories, but in a totally new set-theoretical context. This would be a major conceptual revolution. But this idea of homotopy can also be found at the origin of another, much more tangible, revolution that will eventually allow for the validity of proofs to be checked using computers.

Mathematicians may be currently experiencing the first tremors of an upheaval which will completely transform their way of thinking and working. A revolution that is comparable to that in which quantum physics has eclipsed classical physics.¹⁶ But we may yet need a few generations to see this particular revolution clearly.

Translated from the French by the author.