Fukugen

On Shinichi Mochizuki’s Inter-universal Teichmüller Theory

The sunlight is strong in Kyoto, even in winter. In December of 2014, I visited Shinichi Mochizuki at the Research Institute for Mathematical Sciences to discuss his inter-universal Teichmüller theory (IUT).¹ A distinguished mathematician and a leading figure in anabelian geometry, Mochizuki first made his papers about IUT available at the end of August, 2012. Their study has proved challenging.

A term that is frequently used in mathematical discussions about anabelian geometry and IUT is fukugen, which may be translated as restoration or as reconstruction, and which, like so many words in a foreign language, cannot be truly translated.

It must be used without translation. But isn’t this true of mathematics itself?

Numbers are among the basic concepts of our culture. The most difficult unsolved problems in mathematics are number theoretic. It is easy to see why. The natural numbers are infinite but discrete. The real numbers form a linear continuum. In the late nineteenth century, Georg Cantor demonstrated that there is no one-to-one mapping between the natural and the real numbers. This is still a shocking result. Fundamental changes in mathematics have arisen from the interplay between these structures, and many mathematicians suspect that, at a profound level, the mathematical structures behind the natural numbers are continuous. The history of physics and chemistry suggests as much. The periodic table appears to list a series of discrete atoms, but from the much deeper perspective of quantum field theory, these stable and discrete—indeed, isolated—structures are the adaptive masks worn by continuous fields.

IUT contributes to a new view of the numbers. This may sound as if Mochizuki had announced, rather than executed, a program in pure mathematics. But IUT yields proofs of several outstanding problems in number theory: the strong Szpiro conjecture for elliptic curves, Vojta’s conjecture for hyperbolic curves, and the Frey conjecture for elliptic curves.

And it settles the famous Oesterlé–Masser or abc conjecture.²

The abc conjecture is easy to state and difficult to prove. Prime numbers are defined in terms of multiplication in the ring of integers. A non-zero integer $m$ may be factored into the product of positive integer powers $p_i^{n_i}$ of distinct prime numbers $p_i$, so that $m=\pm \prod p_i^{n_i}$. Let $C\left(m\right)=\prod p_i$ designate the product of all distinct prime divisors $p_i$ of $m.$ In what follows, $C\left(m\right)$ serves as a crude approximation to the absolute value $\left|m\right|$ of $m.$ It is crude because in $C\left(m\right)$, positive exponents are replaced by 1.

It is not easy to get cruder.

The abc conjecture affirms that for every $\epsilon >0$, there is a positive number $\kappa ,$ depending on $\epsilon$, such that for every three non-zero coprime integers $a,b,c$ satisfying $a+b=c$,

$\mathrm{m}\mathrm{a}\mathrm{x}(\left|a\right|,\left|b\right|,\left|c\right|)\le \kappa C{\left(abc\right)}^{1+\epsilon }.$

The abc conjecture expresses a universal asymptotical property of all non-zero integers a and b whose sum is not zero. For finitely many $a,b$, the existence of $\kappa$ is obvious. The crude approximation $C\left(ab\right(a+b\left)\right)$ of $ab(a+b)$, when raised to the degree $1+\epsilon$ for any fixed positive $\epsilon$ close to 0, asymptotically bounds $\left|a\right|,\left|b\right|,|a+b|$ from above.

What gives the abc conjecture its lurid fascination is that it asks about additive relations between prime numbers while their definition uses multiplication only. Michel Waldschmidt put the point nicely (for positive a, b):³

The abc conjecture describes a kind of balance or tension between addition and multiplication, formalizing the observation that when two numbers a and b are divisible by large powers of small primes, a + b tends to be divisible by small powers of large primes.⁴

Stronger versions of the abc conjecture conditionally imply solutions of dozens of famous problems, among them Fermat’s Last Theorem. A proof would occupy only a few lines, modulo the text of IUT, and the proof will be completely different from the first proof by Andrew Wiles.

As one might expect, IUT is not a theory that rewards a casual inspection.

A Whirlwind Tour

The central objects of algebraic number theory are the number fields. These are finite extensions of the rational number field. The rings of integers of number fields generalize the integers. The number fields are one of structures hidden behind the facade of the integers. Using them one can solve many classical problems. Real and complex analytic functions, connected to number theoretical objects, are, of course, the subject of analytic number theory. The most famous example is the Euler–Riemann zeta function, $\zeta \left(s\right)=\prod {\left(1-p^{-s}\right)}^{-1},$ where the product is taken over all positive prime numbers. The Riemann hypothesis is a one hundred and fifty year old conjecture about the zeros of this function. Many mathematicians have searched unsuccessfully for its proof. IUT teaches the importance of working with elliptic and hyperbolic curves over the rational numbers and not just the rational numbers themselves.

Then there is arithmetic geometry. Many problems about the numbers involve polynomial relations. Solutions of polynomial equations with coefficients in various number fields can be studied geometrically by using the theory of arithmetic varieties. They can also be studied in a more general way by using arithmetic schemes. Arithmetic geometry uses geometric and algebraic methods, as well as algebraic and arithmetic versions of topological concepts. It is a field to which Alexander Grothendieck made major contributions.⁵ Pierre Deligne’s proof of the Weil conjectures belongs to arithmetic geometry. These conjectures can be stated in a very simple and classical form using polynomials over finite fields, but their proof uses the sophisticated concepts and methods of arithmetic geometry.

Both arithmetic geometry and analytic number theory involve, to some extent, the sensibility of the continuous. Analysis of aspects of the Riemann hypothesis, or the general Birch and Swinnerton-Dyer conjecture, indicate, or at least suggest, that the structures potentially leading to their solution are not likely to be found in conventional arithmetic geometry or analytic number theory. New number theoretical concepts are required.

Inter-universal Teichmüller Theory offers a new perspective on the numbers by generalizing arithmetic geometry. It works with monoids, or semigroups with an identity element. In this context, IUT studies certain multiplicative deformations that arise with respect to elliptic and hyperbolic curves. It is well known among mathematicians that multiplication is the more fundamental concept.⁶ To study deformations, IUT uses explicitly algorithmic mono-anabelian procedures in which rings and their related structures are deconstructed and then reconstructed. Bounds on the ensuing deformation lead to a proof of the strong Szpiro inequality and, as a consequence, of the abc conjecture.

From Reciprocity to IUT

Suppose that p and q are distinct odd prime numbers. Carl Friedrich Gauss’s quadratic reciprocity theorem states that the equations

$x^2\equiv q \left(mod p\right)$

$x^2\equiv p \left(mod q\right)$

are jointly solvable or unsolvable, unless both p and q leave the remainder 3 when divided by 4. In that case, one equation is solvable, the other, not.⁷ Algebraic number theory eventually produced stunning conceptual generalizations of the quadratic reciprocity law.

At roughly the same time that Gauss was studying modular relationships between prime numbers, Évariste Galois was considering symmetry structures defined over the roots of irreducible polynomials. The modern development of Galois theory involves the use of fields and their automorphisms. Given a finite field extension $L$ of $F$, consider the group of all ring homomorphisms from $L$ to $L$ acting as an identity map on $F$. If its order equals the degree of $L$ over $F$, the extension is called Galois; the ring homomorphisms are called Galois automorphisms; and the group is called the Galois group $G(L/F)$. This group consists of ring theoretic symmetries of $L$ over $F$. Given a field $L$ and a finite group $H$ of its ring automorphisms, its field extension, $L$, over the fixed field $L^H$ is a Galois extension. Its Galois group $G(L/L^H)$ is the original finite group $H$.

For every field $F$, one can combine information about all of its finite Galois extensions into a single group. Such is the absolute Galois group $G_F$ of $F.$ $G_F$ is the inverse limit of Galois groups of finite Galois extensions inside a fixed separable closure of $F$. $G_F$ is a topological group. Its open subgroups are absolute Galois groups of the finite extensions of $F$. Galois extensions are abelian when their automorphisms, like the usual numbers with respect to multiplication, commute with one another.

Kummer theory, developed in the mid-nineteenth century by the German mathematician Ernst Kummer, is related to a question quite natural from a modern point of view. To what extent can information derived from the absolute Galois group $G_F$, with its single operation of group multiplication, be used to recover the field $F$, with its two operations of addition and multiplication? One very partial answer is supplied by elementary Kummer theory. For a field $F$ containing all $n$ roots of the polynomial $X^n-1$, there is a one-to-one correspondence between the finite abelian extensions $L$ of $F$, whose degree divides $n$, and the subgroups $B$ of the multiplicative group $F^{\times }$, which contain the subgroup of nth powers $F^{{\times }^n}$. With such $B$’s, one associates the field extension $L_B=F\left(\sqrt[n]{B}\right)$ of $F$, generated by the nth roots of all elements $b\in B$; the Galois group of $L_B/F$ is isomorphic to ${B/F}^{{\times }^n}$.⁸

Galois theory and number theory meet in class field theory, the main achievement of algebraic number theory. Using objects associated to a ground field, such as a number field $K$, or its completion $K_v$, class field theory describes their abelian extensions.⁹ The field of rational numbers $Q$ is completed most obviously by the field of real numbers R, but it is also completed by the field of the p-adic numbers $Q_p$. The p-adic fields are as important as the field of real numbers.

There are two special class field theories over small number fields: cyclotomic class field theory over rational numbers and complex multiplication class field theory over imaginary quadratic fields. They employ structures related to torsion elements that are not available over general number fields.¹⁰ The existence theorem in class field theory for general number fields was proved by Teiji Takagi one hundred years ago.¹¹

The aim of class field theory is to produce a reciprocity map that is almost a topological isomorphism between the maximal abelian quotient $G_F^{ab}$ of the absolute Galois group $G_F$ of the ground field $F$, and a suitable topological abelian group $M_F$. For a local field $K_v$, the corresponding abelian group is the multiplicative group $K_v^{\times }$ of the local field. For a number field $K$, it is the idele class group ${\mathbb{A}}_K^{\times }/K^{\times }$ of $K$. The notation ${\mathbb{A}}_K^{\times }$ stands for the multiplicative group of invertible elements of the adelic ring ${\mathbb{A}}_K$ of $K$.¹² The topology on these groups is defined very naturally.

The reciprocity map is a functorial continuous homomorphism $M_F\to G_F^{ab}$—a structure that is not quite a homeomorphism, but is not far from being a homeomorphism either. For every finite Galois extension $L/F,$ the reciprocity map induces an isomorphism between the maximal abelian quotient ${G(L/F)}^{ab}$ of the Galois group of $L/F$ and the quotient $M_F/N_{L/F}{M}_L$, where $N_{L/F}$ is the norm map. This reciprocity map is a far-reaching generalization of the quadratic reciprocity law. The global reciprocity map is the product of all local reciprocity maps for all non-equivalent completions of the global field. This product sends $K^{\times }$ to the identity Galois automorphism, which corresponds to the general reciprocity law. The existence theorem in class field theory describes a one-to-one correspondence between open subgroups of $M_F$ (called classes) and finite abelian extensions $L$ of $F$ (called class fields).

Almost Forgotten Treasures

Class field theory has a vast number of applications in number theory.¹³ While algebraic Kummer theory works over any ground field containing sufficiently many roots of unity, class field theory works over number fields and their completions, or more generally, over locally compact non-discrete fields.

Robert Langlands, who together with Alexander Grothendieck has most profoundly influenced the number theory of the last fifty years, has recently made use of some classical ideas in Helmut Hasse’s Klassenkörperbericht (A Report on Class Field Theory). Some modern developments in class field theory are relatively unknown, partially due to insufficient attention paid by mathematicians to the substantial arithmetic features hidden in its standard presentation using group cohomology. Jürgen Neukirch’s explicit reciprocity map, considered as a far reaching extension of the reciprocity map in David Hilbert’s Ninth Problem, is an example.¹⁴ Tomio Kubota’s original and mysterious approach to class field theory is another.¹⁵

The Langlands Program may itself be considered a far-reaching generalization of class field theory, one that treats non-abelian as well as abelian Galois groups.¹⁶ Its point of view is nonetheless quite distinctive. There are no generalized class fields, no explicit description of non-abelian extensions, no generalized reciprocity map.¹⁷ Representation theoretic methods developed earlier in quantum mechanics are used instead. Galois group representations are coordinated with representations of arithmetic objects associated to the ground field in class field theory. In arithmetic versions of the theory, one studies two types of L-functions, each generalizing the Euler–Riemann zeta function. Wiles’s proof of Fermat’s last theorem established a very partial case of the Langlands correspondence for a certain class of elliptic curves over the rational numbers.¹⁸ Major open tasks of the Langlands Program remain unsolved, but there have been exciting recent developments.¹⁹

Anabelian geometry is another generalization of class field theory. While class field theories operate with abelian quotients of Galois groups, and the various Langlands correspondences deal with Galois group representations, anabelian geometry treats the full absolute Galois group. The Neukirch–Ikeda–Uchida theorem is an early result in anabelian geometry. The ring isomorphisms between two number fields $K$ and $K^{\text{'}}$ are derived from topological group isomorphisms between the absolute Galois groups of $K$ and of $K^{\text{'}}$. This reflects a certain rigidity property of the number fields.²⁰ These fields are uniquely determined by less information than one might expect. In this case, the isomorphism class of the absolute Galois group of a number field can restore or reconstruct the isomorphism class of the number field.²¹

We still know much less about the absolute Galois groups of number fields than we might wish, but IUT serves to remind the mathematician, otherwise vexed by a Galois gap in his understanding, that, unlike fields, topological groups are able to pass through certain barriers in arithmetic deformation theory.

It was Grothendieck’s ideas that initiated the anabelian geometric program, which operates with algebraic fundamental groups.²² Grothendieck asked about reconstructing the isomorphism class of a hyperbolic curve over a number field from its algebraic fundamental group.²³ The algebraic fundamental group contains a subgroup, the geometric fundamental group, which is the algebraic fundamental group of the geometric object over an algebraic closure of the field. The quotient group is isomorphic to the absolute Galois group of the field. The proof of Grothendieck’s conjecture and its generalizations was obtained by Mochizuki in 1995, and this result is used in IUT.

Instead of establishing an isomorphism between two fields when their absolute Galois groups are isomorphic, mono-anabelian geometry reconstructs the ring structure of an object (i.e. as a field) from its absolute Galois group, or from an algebraic fundamental group.²⁴ In 2008, Mochizuki showed how to restore a number field from the algebraic fundamental group of a certain hyperbolic curve $C$ over the field.²⁵ The proof deals with a subfield $k$ of the non-Archimedean completion of a number field, and includes a functorial group-theoretic algorithm for reconstructing $k$ as a subfield of the function field of $C$.

The reconstruction consists of several steps. The first takes pride of place because it is the most important: it involves reconstructing surjective maps from the algebraic fundamental group of open sub-schemes of $C$, which are obtained by removing a finite collection of k-rational points, to the algebraic fundamental group of $C$. It is a step employing the Mochizuki–Belyi cuspidalization theory over $k$. It is crucial that this reconstruction is compatible with localization. This is the first explicit reconstruction of the number fields and it is independent of the NIU proof.²⁶

This reconstruction plays a fundamental role in IUT.

Fukugen.

The Szpiro Conjectures

Inter-universal Teichmüller Theory does not directly prove the abc conjecture; but it does prove still more geometric conjectures and they, in turn, imply the abc conjecture. The Szpiro conjecture was historically the first in a set of associated conjectures. It deals with two invariants of an elliptic curve $E$ defined over a number field $K$. Conic curves are given by solutions in $K$ of quadratic equations; elliptic curves, by solutions to cubic equations $Y^2=X^3+aX+b$. Coefficients $a,b$ are in $K$, and, what is more, $4a^3+ 27b^2\ne 0$. The $K$-rational points of an elliptic curve are all solutions $(x:y:z)$ of the homogeneous equation $Y^{2}Z=X^3+aX{Z}^2+b{Z}^3$. The notation $(x:y:z)$, where at least one of $x,y,z$ is non-zero, stands for the equivalence class of proportional triples. The set of all equivalence classes $(x:y:z)$ forms the projective plane. The $K$-rational points $(x:y:z)\in E\left(K\right)$ of the elliptic curve $Y^{2}Z=X^3+aX{Z}^2+b{Z}^3$ are of two types: points $(x:y:1)$ where $x,y$ are solutions of the cubic equation, and the point $\left(0:1:0\right),$ the point at infinity of $E\left(K\right)$. And this is key: it is possible to define addition on $E\left(K\right)$ in such a way that $E\left(K\right)$ becomes an abelian group whose neutral element is the point $\left(0:1:0\right)$.

Suppose that an elliptic curve $E$ over the rational numbers $\mathbb{Q}\mathbb{ }$ is defined by $Y^2=X^3+aX+b$. Coefficients may be rescaled so that $a,b$ are integers. For every prime $p$ we can look at the reduction of $E$ modulo $p$: that is, at solutions $\left(x:y:z\right)$ of $Y^{2}Z\equiv X^3+aX{Z}^2+b{Z}^3$ (mod $p$) in the projective plane over the finite field $\mathbb{Z}/p\mathbb{Z}$. For almost all primes $p$, we obtain in this way an elliptic curve over the finite field $\mathbb{Z}/p\mathbb{Z}$. Positive primes $p_1,\dots ,p_n$ for which this is not true are exactly the prime divisors of the discriminant, –$16(4a^3+27b^2)$; the corresponding reduction is called a bad reduction, while $p_i$ are called the bad reduction primes.

By allowing linear transformations of the variables $Y^{\text{'}}=d^{3}Y+f{d}^{2}X+g,X^{\text{'}}=d^{2}X+e$ with coefficients in $K$, one can work more generally with Weierstrass equations $Y^2+a_{1}XY+a_{3}Y=X^3+a_2{X}^2 +a_{4}X+a_6$. It is, of course, possible to define the discriminant of the Weierstrass equation as well. By making linear changes to the variables $X,Y$ with rational coefficients, it is then possible to transform the Weierstrass equation into an equation in integers $a_i$, and the discriminant $∆$ such that for every prime number $p$, the maximal power of $p$ that divides $∆$ divides the discriminant of every other transformed Weierstrass equation whose rational coefficients $a_i$ do not involve negative powers of $p$. If $∆$ is the minimal discriminant of $E$, denote its absolute value by $D_E$. $∆$ can be viewed as a refined approximation to the complexity of $E$. Given that $D_E=\prod p_i^{n_i}$, then the $n_i$’s are certain geometric invariants of the reduction of $E$ at $p_i$. To elliptic curves with so called split multiplicative reduction at $p_i$ one can associate a geometric object in the shape of $n_i$-gon. One also forms a certain product $\prod p_i^{f_i}$ called the conductor $C_E$ of $E$. In the case of elliptic curves with a split multiplicative reduction at $p_i$, all $f_i=1$, and the conductor is the minimal positive integer such that every prime of bad reduction is its factor. We can view the conductor as the first crude approximation to the complexity of $E$.

The Szpiro conjecture for elliptic curves $E$ over rational numbers tells that for every $\epsilon >0$ there is a positive real number $\kappa$, depending on $\epsilon$ but not on $E$, such that for all elliptic curves $E$ over rational numbers

$D_E\le \kappa C_E^{6+\epsilon }.$

Instead of $1+\epsilon$ in the abc conjecture for integers, elliptic curve invariants require $6+\epsilon$, the number 6 playing an important, if somewhat inscrutable, role in what follows.²⁷ In the case of elliptic curves $E$ whose bad reduction is a split multiplicative reduction, one can define a kind of rotation of the $n_i$-gons. Consider this done. IUT then implies that these rotations are synchronized, like working windmills revolving placidly in the presence of wind.²⁸

The strong Szpiro conjecture over number fields now emerges naturally. Let $E$ be an elliptic curve defined over any number field $K$. One can define the minimal discriminant and conductor of $E$ as ideals of the ring of integers of $K$. Denote by $D_E$ and $C_E$ the indices of the minimal discriminant and conductor in the ring of integers of $K$. The strong Szpiro conjecture affirms that for every $\epsilon >0$ there is a positive real number $\kappa$, depending on $\epsilon$, such that for all number fields $K$ and elliptic curves $E$ over $K$

$D_E\le \kappa {\left(C_E{D}_K\right)}^{6+\epsilon }.$

Here $D_K$ is the absolute value of the discriminant of $K$, which measures the complexity of $K$.

The strong Szpiro conjecture implies that every curve of genus $>1$ defined over an algebraic number field has only finitely many rational points. This is the Mordell conjecture. There are several proofs, the first by Gerd Faltings, and then a very interesting one by Paul Vojta, using some analogies with Nevanlinna theory. Rolf Nevanlinna and Oswald Teichmüller knew of each other’s work and there are certain links between their theories. One can ask if there are links between arithmetic generalizations of their works, i.e. Vojta’s proof and IUT. It is well known that the abc inequality implies that there exists a positive integer $n_0$ such that the Fermat equation $X^n+Y^n=Z^n$ does not have positive integer solutions for any $n\ge n_0$. In order to derive a new proof of Fermat’s last theorem, it would be necessary to make $n_0$ explicit, a development suggested by Mochizuki.²⁹

Elliptic curves over number fields mark one of the fundamental boundaries of modern mathematical knowledge. To enlarge this boundary, entirely new concepts, ideas and methods are needed.

Several of them come from IUT.

Monoids

Inter-universal Teichmüller Theory has a number of features that suggest complex Teichmüller theory, but it operates within a different mathematical universe.³⁰ In IUT, there is a fixed, given elliptic curve $E$ over a number field $F$. The elliptic curve is assumed to be of sufficiently general type and with sufficiently good properties, in particular, each of its bad reductions is split multiplicative reduction. Given a prime number $l$, IUT uses $l$-torsion points of the elliptic curve $E$, i.e. points whose $l$-multiple with respect to the group operation on $E$ is the zero element of the group. In some sense, the use of the finite field ${\mathbb{F}}_l=\mathbb{Z}/l\mathbb{Z}$ can be viewed in IUT as an approximation to the ring of integers. IUT intensively operates with several associated hyperbolic curves, such as the punctured elliptic curve $E$ without its zero element, or $E$ without all its $l$-torsion points. These hyperbolic curves are used to recover the ring structure of the number fields using the algorithms of mono-anabelian geometry.

A monoid is a set with binary associative operation and an identity element. Certain monoids are subsets within groups obeying their associative operation. For example, the multiplicative group ${\mathbb{Q}}_p^{\times }$ of the field ${\mathbb{Q}}_p$ of p-adic numbers splits into the product of the group of units ${\mathbb{Z}}_p^{\times }$ and the infinite cyclic group generated by $p$. One can also consider the multiplicative monoid ${\mathbb{Z}}_p\backslash \left\{0\right\}$ of p-adic integers; this monoid splits into the product of ${\mathbb{Z}}_p^{\times }$ and the multiplicative monoid of non-negative integer powers of $p$.

Another example, which plays an important role in the theory of Frobenioids, is a non-commutative monoid $\mathcal{F}$ of elements $(a,n)$, where $a\ge 0$ and $n>0$ are integers. The requisite associative operation is $(a,n)(a^{\text{'}},n^{\text{'}})=(a+n{a}^{\text{'}},n{n}^{\text{'}})$. Elements $(a,n)$ of $\mathcal{F}$ have Frobenius degree $n$. It is easy to show that any monoid homomorphism from $\mathcal{F}$ to a finite group $G$ factors through the natural surjection $(a,n)⟼n$. Mochizuki’s theory of frobenioids is an example of a combinatorial blunt force applied to the structures of scheme-theoretic arithmetic geometry. The abstract combinatorial structure of a monoid, derived in turn from a ring, reveals essential ring-theoretic properties without an appeal to ring theory itself.³¹ A remarkable subtle intellectual maneuver is involved in which something is used—the ring—and then forgotten—ring? What ring?—and then recovered—the ring.

IUT works with various monoids and the Galois action on them. Consider the ring $O$ of integers of an algebraic closure of a local field, together with the action of the absolute Galois group $G$. One can then consider multiplicative monoids $O^{⊳}$ of the set of integers with zero removed, and the group $O^{\times }$ of their units. The map that sends $(G,O^{⊳})$ to $G$ induces a bijection from the group of automorphisms of $(G,O^{⊳})$ to the group of automorphisms of the topological group $G$. The map that sends $(G,O^{\times })$ to $G$ induces a nontrivial kernel on the associated groups of automorphisms.³²

Monoid-theoretic structures are of essential importance in IUT; they make possible various gluing isomorphisms that are impossible at the level of arithmetic geometry. Two structures $(G_1,O_1^{⊳})$, $(G_2,O_2^{⊳})$ can be glued by means of an arbitrary isomorphism $(G_1,O_1^{\times })\to (G_2,O_2^{\times })$. Describing the structures naturally associated to $(G_1,O_1^{⊳})$ using only $\left(G_2,O_2^{⊳}\right)\mathrm{ }$ is a highly non-trivial problem.

Working with hyperbolic curves over number fields adds a geometric dimension to the arithmetic dimension of the field. IUT forges a connection of sorts between the two dimensions of a hyperbolic curve and the two combinatorial dimensions of the field $\left(F,+\times \right)$ corresponding to its additive structure and multiplicative structure.

IUT is profoundly concerned with the deconstruction and reconstruction of the two underlying dimensions of a number field. Certain walls are impassable for rings. But fundamental and Galois groups pass right on through. This is deconstruction. Mono-anabelian geometry reconveys the field’s structure from a consideration of its ancillary groups. And this is reconstruction.

A manifestation of the flow of fukugen.³³

Examples of deconstruction include: (a) the splittings of various local monoids into units and value group portions; (b) the separation of the finite field ${\mathbb{F}}_l$ into additive and multiplicative symmetries; and (c) the separation of ring structures into their respective underlying additive and multiplicative structures.

Reconstruction shows to what extent two dismantled combinatorial dimensions cannot be separated. It does this by describing the intertwining structure between the two dimensions before their separation. This procedure allows one to estimate the value group portions of various monoids in terms of their unit group portions.

At bad reduction primes $v$, rational points $E\left(F_v\right)$ of $E$ in the completion $F_v$ of $F$, can be viewed as the quotient of the multiplicative group $F_v^{\times }$ by the free group generated by a certain element $q$ of the maximal ideal of the local integral ring. This element $q$ is the analogue of $p_i^{n_i}$ in the Szpiro inequality. One then works with a non-Archimedean theta-function

$\theta \left(u\right)=\sum _{n\in \mathbb{Z}}{\left(-1\right)}^n{q}^{n(n-1)/2}{u}^n=\left(1-u\right)\prod _{n\ge 1}\left(\left(1-q^n\right)\left(1-q^{n}u\right)\left(1-q^n{u}^{-1}\right)\right),$

where $u$ is a non-zero element in the algebraic closure of $F_v$. The last equality follows from the Jacobi triple product formula. The functional equation $\theta \left(u\right)=-u\theta \left(qu\right)$ is obvious. Thus, for any integer $m$, $q^{\left(m^2-m\right)/2}=\theta \left(-1\right)/\theta \left(-q^m\right)$. This relation is used to represent powers of $q$ as special values of a modified theta-function. IUT shows that these values are very special. Many properties of $\theta$ are similar to the properties of the classical complex valued theta-function. The non-Archimedean theta-function is both a kind of analytic object, and a more algebraic and geometric object than a complex-valued theta function.

The study of $\theta$ substantially extends two classical works: John Tate’s work on theta functions and David Mumford’s theory of theta groups and algebraic theta functions. IUT uses a generalized but truncated form of Kummer theory in which line bundles are associated to non-Archimedean theta-functions. This theory creates a bridge between monoid-theoretic and fundamental group structures.

It is from this generalized Kummer theory that one can derive an anabelian construction of the Kummer class of $\theta$. Three new rigidity properties now appear. They are properties of a certain category-theoretic invariant of the fundamental group of the punctured $E$ over $F_v$. It is useful to coin the phrase rigidities to serve in place of the ungainly rigidity properties. The rigidities are, in the first place, a discrete rigidity; in the second, a constant multiple rigidity; and, in the third, a cyclotomic rigidity.³⁴ The first implies that one can deal with integer powers, instead of $\widehat{\mathbb{Z}}$-powers of divisors, on those coverings of $E\left(F_v\right)$ studied in IUT; the second provides a canonical splitting of monoids related to the theta-function; and the third exploits the fact that the commutator of associated theta groups is exactly of degree 2.

There are two symmetries for hyperbolic curves associated to an elliptic curve over a number field. We might as well call them Symmetry One and Symmetry Two. They are denoted as

${\mathbb{F}}_l^{⋊\pm }={\mathbb{F}}_l⋊\left\{\pm 1\right\}, {\mathbb{F}}_l^{\divideontimes }={\mathbb{F}}_l^{\times }/\left\{\pm 1\right\},$

with ${\mathbb{F}}_l$ arising from the $l$-torsion points of $E$. Elements of ${\mathbb{F}}_l$ (in the case of ${\mathbb{F}}_l^{⋊\pm }$) or ${\mathbb{F}}_l^{\divideontimes }$ (in the case of ${\mathbb{F}}_l^{\divideontimes }$) are called labels. Labels may be glued: $\pm a\in \left\{-\left(l-1\right)/2,\dots ,-\mathrm{1,0},1,\dots ,\left(l-1\right)/2\right\}$ is identified with $a\in \left\{1,\dots ,\left(l-1\right)/2\right\}$.

Symmetry One arises from the action of the geometric fundamental group and is closely related to the Kummer theory for theta-values. This additive symmetry is of an essentially geometric nature. Symmetry Two arises from the action of the absolute Galois group of certain number fields and is also closely related to the relevant Kummer theory. This multiplicative symmetry is arithmetic. These symmetries are coded in appropriate theatres. The two types of symmetry require the use of finite fields.

There are various informal analogies between Symmetry One and Two in IUT and the two adelic structures in two-dimensional adelic geometry, even though the theories fundamentally differ from each other.³⁵ In IUT, it is necessary to isolate the two types of symmetry in order to work with global base fields using the ${\mathbb{F}}_l^{\divideontimes }$–symmetry; and in order to establish certain conjugate synchronizations using the ${\mathbb{F}}_l^{⋊\pm }$-symmetry. Divide and conquer. Conjugate synchronization is a specific system of isomorphisms between local absolute Galois groups. Given conjugate synchronization, Kummer theory is then applied to several special values of the theta-function.

In the specific situation of the elliptic curve $E$ over the number field $F$ and the prime number $l$, IUT operates with Hodge theatres—categorical objects generalizing some aspects of the original arithmetic and geometry. These radically new concepts were invented by Mochizuki.

Theatres represent a system of categories obtained by gluing categories over a base. Many of these base categories are isomorphic to the full subcategory of finite étale covers of hyperbolic curves. Each theatre consists of two portions, or sides, corresponding to Symmetry One and Symmetry Two. In IUT, they are glued together in a way compatible with the gluing of their labels. The object that results goes beyond conventional arithmetic geometry. It is important that each type of symmetry includes a global portion related to the number field and the hyperbolic curves over it. They might be compared to the way in which elements $K^{\times }$ sit inside ideles ${\mathbb{A}}_K^{\times }$ in class field theory.

With theatres, arithmetic deformation becomes possible as an idea and as a technique. An example of deformation on a local field, say the field of $p$-adic numbers ${\mathbb{Q}}_p$, is a map that for a fixed $m$ sends $p^{j}u$ to $p^{jm}u$ for all units $u$ of ${\mathbb{Z}}_p$. While this map is a morphism of multiplicative structures, it is evidently not compatible with addition.

IUT studies certain non-ring-theoretical relations, links between theatres. The only type of mathematical object that makes sense in the domain and codomain of such a link is a topological group—the abstract topological group underlying a Galois group, for example.

Monoid-theoretic structures that appear in theta-links consist of two local structures: units of the ring of integers of a local field and theta values defined up to multiplication by roots of order dividing $2l$. At bad reduction primes, the theta link includes assignments on the multiplicative group of the relevant local field. The theta-links go two by two: there are two distinct ring-scheme theories, and two theatres in the domain and codomain of the theta-link, their multiplicative structures related at bad reduction valuations via non-Archimedean theta values. The theta-link requires the use of a non-Archimedean logarithm map defined on units of the ring of integers. The map sends $1-x⟼-{\sum }_{n\ge 1}{x}^n/n$ for $x$ in the maximal ideal of the ring of integers, and sends roots of unity to 0. The logarithm is compatible with Galois automorphisms.

The curious and compelling point is that the logarithm transforms multiplication into addition, and thus permits the recovery of additive from multiplicative structures.

Fukugen.

Mutually Alien

Deconstruction of ring structures proceeds when the underlying additive and multiplicative structures of the ring are treated as separate monoid-theoretic structures. Ring structures are reconstructed by means of a series of algorithms using results from anabelian geometry and generalized Kummer theory. From the point of view of the internal ring structure of the codomain of the theta-link, the internal ring structure in the domain of the theta-link is a black box.

The two ring structures are, within IUT, said to be mutually alien.

Arithmetic deformation theory is charged in IUT with the task of explaining how much the additive structures of ambient rings differ. Generalized Kummer theory and mono-anabelian reconstruction algorithms are suited to this end, and they eventually make it possible to compare the left and right hand sides of the strong Szpiro inequality.

One of the main aims of IUT is the study of mathematical structures associated with a two-dimensional log-theta-lattice. These are formed by theatres ${\mathcal{T}}_{n,m}$ in which there are upward-pointing vertical log-links, and rightward-pointing horizontal theta-links. This lattice is not commutative.

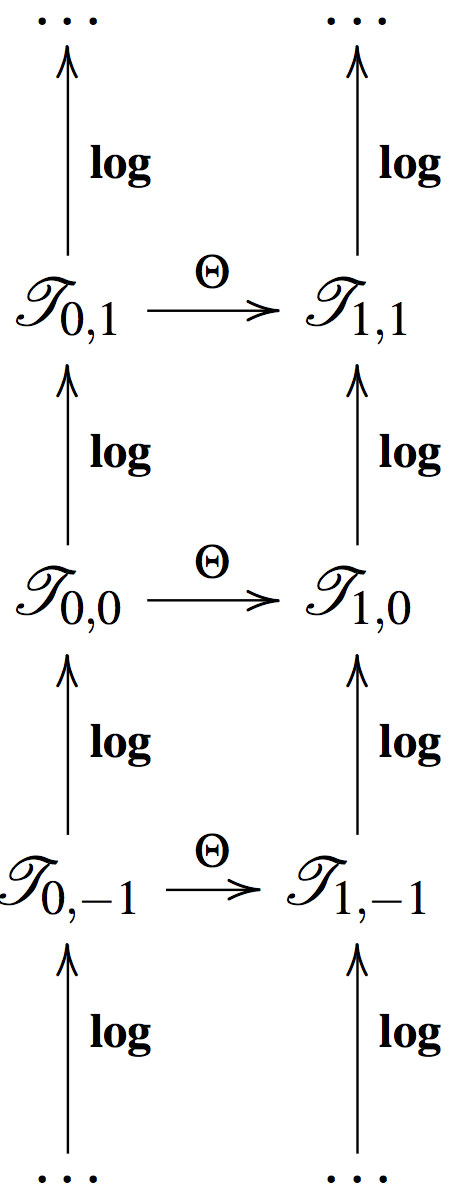
Each of the vertical arrows ${\mathcal{T}}_{n,m}\to {\mathcal{T}}_{n,m+1}$ corresponds to an application of the log-link, and each of the horizontal arrows ${\mathcal{T}}_{n,m}\to {\mathcal{T}}_{n+1,m}$, to the theta-link. There is no natural action of the theta-values on the multiplicative monoid of units modulo torsion, but there is a natural action of the theta-values on the logarithmic image of this multiplicative monoid. The multiplicative structures on either side of the theta-link are related by means of the value group portions; the additive structures on either side of the theta-link are related by means of the unit group portions; these are shifted once via the log-link in order to transform the multiplicative structure of these units group portions into an additive structure.

To define the power series logarithm for the log-link, ring structures are needed, but the theta-link is not compatible with ring structures. From the point of view of the codomain of $\mathrm{\Theta }:{\mathcal{T}}_{n,m}\to {\mathcal{T}}_{n+1,m}$, one can only see the units group and value group portions of the data that appears in the domain of this theta-link. Applying the log-link ${\mathcal{T}}_{n,m-1}\to {\mathcal{T}}_{n,m}$ yields the value group portion at ${\mathcal{T}}_{n,m}$. Thus, one is led to consider structures that are invariant with respect to arbitrary vertical shifts ${\mathcal{T}}_{n,m-1}\to {\mathcal{T}}_{n,m}$. These log-shells are a common structure for the log-links in one vertical line. Its non-Archimedean part is an image of the local units via the non-Archimedean logarithm; the log-shell associated to a complex Archimedean field is the closed ball of radius $\pi$.

The main results of IUT require the use of two bi-infinite and neighboring vertical lines of lattice arrows: those corresponding to the lattice points $(n,m)$, where $n$ equals 0 or 1, together with the horizontal arrow from ${\mathcal{T}}_{\mathrm{0,0}}$ to ${\mathcal{T}}_{\mathrm{1,0}}$.

Algebraic fundamental groups depend, up to conjugation, on the choice of their base point. The existence of different base points in the domain and range of the theta-link and log-link implies that one must consider two different universes associated to two distinct ring theories (hence the name of IUT!); these in general cannot be related by means of a ring homomorphism. The main type of mathematical object that makes simultaneous sense in both universes is a topological group, such as the topological group of an arithmetic fundamental group or a Galois group.

IUT applies mono-anabelian reconstruction algorithms to algebraic fundamental groups that appear in one universe in order to obtain descriptions of objects constructed from such algebraic fundamental groups that make sense in another. Mochizuki has used the image of a wheel and spokes. One can think of reconstruction algorithms as functorial algorithms from a radial category to the center category. Descriptions of objects on one spoke must make sense from the point of view of another spoke. A functorial algorithm is called multiradial if it expresses objects constructed from a given spoke in terms of objects that make sense from the point of view of other spokes. It is important that the generalized Kummer theory used in IUT be multiradial.

To obtain multiradial algorithms, it may be necessary to allow some sort of descriptive indeterminacy in the algorithms constructing objects from a given spoke. There are three indeterminacies that can be viewed as the effects of arithmetic deformation. They play a key role in the computation of volume deformation, and they result in the $\epsilon$ term in the Szpiro conjectures.³⁶

The first indeterminacy is related to the absolute Galois group automorphisms of a local field; it indicates that those automorphisms are compatible with the permutation symmetries of the Galois and arithmetic fundamental groups that are associated with the vertical lines of the log-theta-lattice.

The second indeterminacy is related to the action of a certain compact group of isometries on the logarithmic image of units. It comes from the requirement of compatibility with the horizontal theta-link.

The third indeterminacy comes about because Kummer isomorphisms must be compatible with the log-links associated to a single vertical line of the log-theta-lattice.

Taking into account the three indeterminacies and making a suitable choice for the prime number l helps to bound the size of the deformation arising from the theta-link. A further computation leads to a bound of the type needed for the strong Szpiro conjecture and the Vojta hyperbolic conjecture.

Model theorists were the first to react to IUT. Some of the reconstruction theorems may be understood in terms of a logical interpretation. The concept of multiradiality may be understood in terms of definability. It is possible to imagine a certain model of theoretic mono-abelian geometry.

Mathematicians working with one element field theoretic geometry or studying arithmetical homotopy theory have also been interested in IUT.

Why categories in IUT, and why no maps between sets? These are questions raised in arithmetic geometry more than 40 years ago. IUT works with algebraic fundamental groups, so one must use categories. This was a message imparted by Grothendieck, but Grothendieck’s work has not really appeared as manna from heaven to all number theorists. Having been deprived of manna, they are slow in digesting IUT.³⁷

It happens.

On the other hand, IUT does not deal directly with the Archimedean aspects of various inequalities by using non-scheme-theoretic analytic number theory. The center of activity is shifted to non-Archimedean data by means of the product formula. The resulting theory is not scheme-theoretic.³⁸ In this sense of containing an important non-scheme-theoretical core, IUT is nearer to analytic considerations in number theory than anything provided by conventional arithmetic geometry.

IUT is different in its philosophy and main ideas from anything we have known in conventional number theory. It is already changing mathematics, and as more people learn and develop IUT, this will continue.³⁹

It takes time for this to happen.

I am grateful to Shinichi Mochizuki for numerous valuable discussions and to David Berlinski for his stimulating ideas about the presentation of IUT. I am thankful to Edward Frenkel, Kobi Kremnitzer, Laurent Lafforgue, Robert Langlands, Yuri Manin, Sergey Oblezin, Richard Thomas and Boris Zilber for their comments and suggestions on earlier versions of this text.