The muon is an elementary particle. It has the same electric charge and spin as the electron, but it is about two hundred times heavier. It was unexpected when observed in cosmic ray experiments in 1936.
“Who ordered that?” Isidor Rabi asked.1
Muons and electrons behave as if they are tiny electrically charged magnets. The magnitude of their magnetic moments is given by the ratio of the electric charge to twice their mass times a dimensionless parameter g—the gyromagnetic ratio. Paul Dirac’s relativistic quantum mechanics equation fixes the value of g at 2 for both electrons and muons. The development of quantum electrodynamics imposed radiative corrections on the value of g. Its precise value is slightly different for electrons and muons, not precisely 2 in either case. Dirac’s result is simply the first term in a perturbative expansion.2
The quantum field theory formulation of electrodynamics (QED) was developed after the Second World War by Richard Feynman, Julian Schwinger, and Sin-Itiro Tomonaga.3 Results in QED are obtained by series expansion over powers of the dimensionless fine structure constant α. The measured reciprocal of α is 137.035999046(27), one of the very few quantities in nature whose value is known to ten decimal places.4 Schwinger used QED to determine the lowest order radiative correction to Dirac’s value for the gyromagnetic ratio of any charged lepton:
a≡12(g−2)=α2π≃ 0.001166 … ,
where a is a measure of the departure of g from its zeroth-order value of 2.5
The prediction was soon confirmed by a measurement of the electron anomaly ae to a level of 4% precision.6
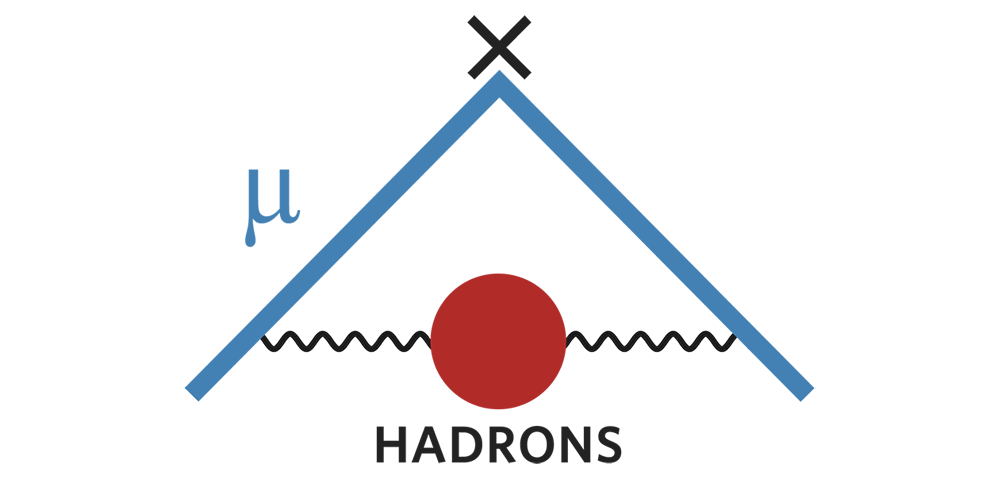
Schwinger’s calculation represents the emission by a charged lepton in a magnetic field of an unobserved particle of light—a virtual photon—that is later reabsorbed by the lepton. The propagation of this virtual photon, illustrated by the Feynman diagram in Figure 1, generates a correction to the Dirac g = 2 result and hence an anomalous magnetic moment called the anomaly a.
Figure 1.
Feynman diagram corresponding to the Schwinger contribution in the equation above. The X in the muon μ (blue line) represents the external magnetic field. The black wavy line represents the propagating virtual photon.
Schwinger’s result applies to any spin-½ charged particle or antiparticle; it is the same for the electron and the muon as well as the tau lepton, which has a higher mass, because g is a dimensionless number.7 In his calculation, a massless photon is emitted prior to the particle’s interaction with an external magnetic field and is absorbed afterward. No mass scale is involved other than that of the particle involved. Theorists have calculated corrections to Schwinger’s one-loop order-α result, involving additional loops and powers of α, as the precision of experimental measurements has increased. These corrections are now known in terms of exact mathematical quantities up to order (απ)3, and at good numerical approximations up to (απ)5, which is extraordinary. The analytic evaluation of the coefficients of this series in (απ) powers involves higher and higher transcendental numbers, such as integral values of the Riemann zeta function, showing once more the beautiful relationship between mathematics and physics.
The values of the electron and the muon anomalies ae and aμ differ at the order of the (απ)2 and higher power contributions because of quantum vacuum fluctuations induced by other particles. Quantum fluctuations induced by charged lepton–antilepton pairs are calculable using QED techniques.8 Such fluctuations can be induced by all the particles of the electroweak theory of the Standard Model—charged leptons with their associated neutrinos, quarks and gluons, the heavy gauge W and Z bosons, as well as Higgs particles. They all contribute to the muon anomaly aμ. These quantum fluctuations can be evaluated in the Standard Model because this theory,9 when combined with the Higgs-particle mechanism,10 is renormalizable.11 Observables can be calculated without parameters other than those already present in the initial formulation of the theory.
The contribution to aμ from hadron quantum fluctuations—strongly interacting particles like pions and protons—is not straightforward. Calculation requires the underlying theory of the strong interactions, quantum chromodynamics (QCD), figuring at all energy scales and, in particular, at the low energies and long distances at which the fundamental quarks and gluon-gauge particles of QCD are confined and condense into the observed hadronic particles. Theorists do not have as yet a full dynamical understanding of confinement. They resort either to phenomenological estimates, or to numerical simulations of the underlying dynamics of QCD theory made in discrete lattices of the space-time continuum. Implemented in some of the world’s most powerful supercomputers, these simulations involve sophisticated techniques that have been developed under the name of lattice QCD (LQCD).12 LQCD simulations in smaller and smaller space-time lattices of larger and larger volumes have already produced impressive results in hadron physics.13
Two dedicated experiments have provided precise measurements of the muon magnetic moment anomaly, one at the Brookhaven National Laboratory (BNL) the other at Fermilab (FNAL). These labs give the results
aBNLμ = 116,592,089(63) × 10–11
and
aFNALμ = 116,592,040(54) × 10–11.14
They agree with each other at the level of 0.6σ (0.6 standard deviations), and their combined result,
aμ(2021) = 116,592,061(41) × 10–11 (0.35 ppm),
is accurate to 0.35 parts per million (ppm).
The theoretical evaluation of the same observable in the Standard Model, if made at a comparable level of precision, involves many subtle details about the interaction dynamics of all Standard Model particles, as well as high precision measurements in atomic physics.
It requires a total knowledge of the relevant physics.
The failure to reproduce the experimental results would constitute strong evidence for physics lying beyond the Standard Model.
What do physicists know for sure about this confrontation?
Measurements of the Muon Anomalous Magnetic Moment
The clever experimental determination of the anomalous magnetic moment of the muon aμ is based on three fundamental physical properties:
- Muons produced by the decay of pions are longitudinally polarized: the positively charged muons in the FNAL experiment have their spins oriented opposite to their momenta.
- The orbit frequency of a muon turning in a horizontal storage ring in the presence of a uniform vertical magnetic field differs from its spin precession by a factor precisely proportional to the muon anomalous magnetic moment aμ that one wants to measure. This difference is called the anomalous precession frequency.
- Muons, like pions, are unstable particles and have a lifetime at rest of about two microseconds. Their weak decay into an electron and two neutrinos violates parity, and this provides the trick to measuring the anomalous precession frequency, hence the muon anomalous magnetic moment.
The trick succeeds because the muon spins are strongly correlated with the decay electron momenta. This spin-energy correlation results in a modulation of the electron decay energy spectrum that occurs at the rate of the anomalous precession frequency, and this is how the anomaly is measured.
In practice, one needs good statistics of a pion source. This is provided by the proton collisions emerging from a high energy accelerator, and for this reason, the experiments have been made at places such as CERN, BNL, and FNAL. The polarized muons from pion decays are then boosted in a storage ring, so as to sufficiently increase their lifetimes, in the presence of a very precise homogeneous vertical magnetic field and an inner ring of energy detectors measuring the electron decay from the stored muons. This approach was pioneered in a series of dedicated experiments at CERN between 1962 and 1968, which were further pursued by the E821 experiment at BNL and recently by the FNAL muon g – 2 experiment, which is still underway.15
Vacuum Polarization Effects
Vacuum polarization is a characteristic phenomenon arising in the quantum formulation of electrodynamics. First discussed by Dirac and Werner Heisenberg, it occurs when a virtual photon propagating between two sources probes a vacuum fluctuation of electrically charged particle–antiparticle pairs.16 These particles can be leptons or quark–antiquark pairs. Observable effects of vacuum polarization in atomic physics were first evaluated to lowest order in powers of the fine structure constant α by Robert Serber and Edwin Uehling in 1935.17 In QED, Feynman, Schwinger, Tomonaga, and Dyson showed how to do systematic calculations of these effects in powers of the small coupling constant α and, in particular, how to evaluate the QED contributions to the lepton anomalies. The lepton vacuum polarization effects (lepton-VP) to aμ induced by muon–antimuon pairs give mass-independent contributions, since g is massless and the only mass in this case is that of the muon. Those induced by tau–antitau pairs decouple by a factor m2μM2τ because virtual photons coming from the external muon carry an average momentum too small to probe the heavy tau–antitau pairs from the vacuum. The lepton-VP effects induced by the vacuum fluctuations of electron–positron pairs are large because the average momentum carried by the virtual photon emitted by the external muon is large compared to the electron mass. This produces a logmμme ~ 5 factor at the (απ)2 order of the QED contribution and higher logmμme powers at higher orders. These give rise to large contributions to the total theoretical budget. Although the calculations are technically difficult, they have been done analytically and in some cases numerically to the needed accuracy, mostly by Toichiro Kinoshita and his collaborators.18
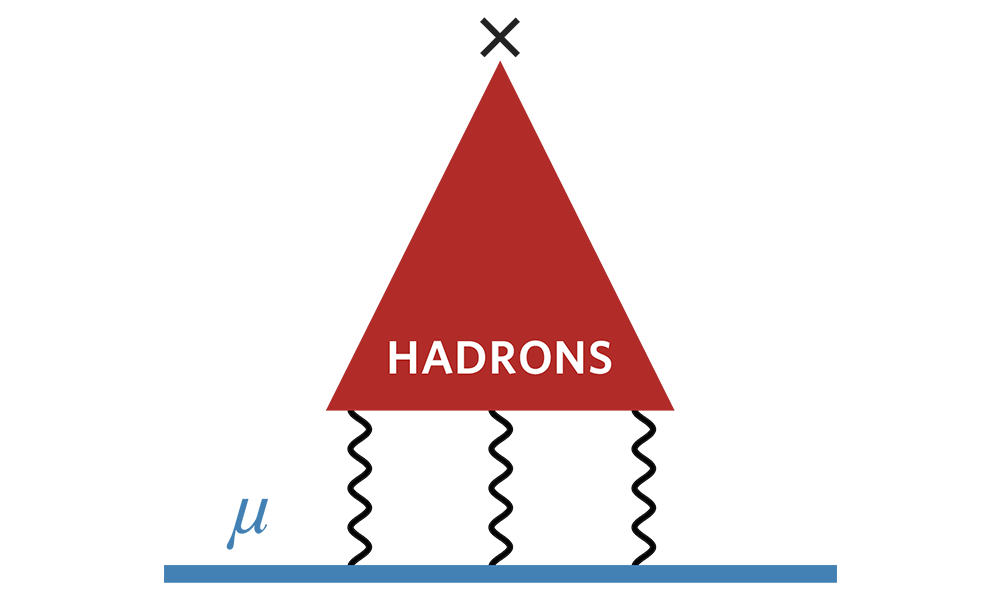
Vacuum polarization resulting from lepton–antilepton loops was first considered in the context of QED. However, every charged particle contributes to vacuum polarization. Hadronic vacuum polarization (HVP) is due to hadron–antihadron loops. Its evaluation is not straightforward because hadrons are subject to strong QCD forces, but its magnitude can easily be estimated: it appears first at the level of the (απ)2 contributions because, as illustrated by the Feynman diagram in Figure 2, at least two virtual photon propagators, represented by the wavy lines, are needed to connect to the hadron–antihadron loop indicated by the disk. The virtual photons in this case carry an average momentum that is small compared to the masses of the hadronic particles that they can probe. Because of spin symmetry properties, the overall effect must be modulated by a mass factor m2μ, which, in order to make g dimensionless, must be normalized to another mass scale, which is expected to have the size of the mass of the lowest lying hadronic resonance to which the photons can couple. This is the ρ(770 MeV) particle. The overall m2μ dependence makes the g factor of the muon more sensitive to hadronic effects than the electron by a ratio m2μm2e≃ 43,000. The muon anomaly is much more sensitive to effects beyond those encoded in the Standard Model, and these may be contributing to vacuum polarization. This is the reason for the interest in a precise determination of aμ.
The estimated order of magnitude, (απ)2m2μM2ρ∼ 10–7, of the HVP contribution seems rather small, but it is big enough when compared to the 0.35 ppm accuracy reached in recent experimental determinations of aμ. It requires more attention than just an order of magnitude evaluation.
Figure 2.
Feynman diagram of the HVP contribution. The X in the muon line represents the external magnetic field.
The HVP contribution to aμ is called aμ(HVP). Its evaluation depends critically on the hadronic forces generated by QCD, whose effects cannot be perturbatively calculated, but which are described by an analytic function ΠHVP(q2) of the energy-momentum squared of the virtual photon. This function encodes how photons interact via QCD with hadrons. The contribution to aμ(HVP) due to hadron loops is given by q2-range dependence of ΠHVP(q2). Cauchy’s integral theorem shows how to evaluate ΠHVP(q2) everywhere once its shape on the real axis is known from the hadronic threshold at q2 = 4m2π, where mπ is the mass of a charged pion, to the spectral function region at infinity. It turns out that it is precisely over a large range of this spectral function region that ΠHVP(q2) is accessible to experimental determination by means of the total cross section that emerges when electrons and positrons annihilate, thereby producing hadrons. Furthermore, the shape of the spectral function in the very high q2 energy region, where there is no more experimental information, is well predicted by the asymptotic freedom property of QCD.19
The precise wording of aμ(HVP), what is now called the dispersive HVP evaluation of aμ, was first given by Claude Bouchiat and my thesis advisor Louis Michel in 1961.20 In 1969, using the results from experiments at the Linear Accelerator in Orsay, a first quantitative evaluation was made at the level of 8% accuracy, which was sufficient for an overall comparison with the experimental value of aμ.21 With the advent of increasingly refined experiments on e+e– annihilations into hadrons, the precision of the HVP contribution to aμ has improved considerably. The most recent determination, made by Michel Davier and collaborators from dedicated experiments at several facilities, quotes a precision level of 0.5%.22 In spite of this accuracy, it still remains the one that at present has the largest error.
Alternative and increasingly accurate evaluations of the aμ(HVP) contribution have been made during the last few years using LQCD techniques, and, in fact, the recent results published by the BMW collaboration are comparable to the dispersive evaluations.23
Light-by-Light Scattering Effects
The scattering of light off light (LbyLS) is another rare phenomenon that only happens at the quantum level and is predicted by QED. It has been recently detected at the Large Hadron Collider at CERN, but it also occurs due to the vacuum fluctuations induced by the effect of four photons. LbyLS contributes to aμ at the order of (απ)3 because, in the presence of an external magnetic field, as seen as one photon, an incoming external muon can emit and reabsorb three virtual photons that simultaneously—one + three—probe the vacuum fluctuation of leptons and/or hadrons. The Feynman diagram in Figure 3 illustrates this process; the red triangle represents either leptons or hadrons.
As for the lepton-VP effects discussed earlier, the LbyLS induced by muon loops yields mass-independent contributions to aμ. These have been calculated to the needed accuracy either numerically or analytically.24 Those arising from tau-lepton loops also decouple like those of lepton-VP and are very small. Those arising from electron loops turn out to be very important giving a π2 log mμme factor at the leading (απ)3 level.25 This came as a big surprise in 1969 because in QED, the LbyLS does not have an intrinsic new coupling constant beyond its electric charge coupling e4 to the four photons and, therefore, does not require renormalization. This is in contrast to the vacuum polarization calculation discussed earlier. The unexpectedly large LbyLS contribution served to eliminate a possible discrepancy between theory and experiment.26
Figure 3.
Feynman diagram of the hadronic LbyLS contribution.
Hadronic light-by-light scattering (HLbyL) is the corresponding effect induced by hadron loops, and its evaluation is not as straightforward as the one induced by leptons because QCD must be dealt with. Furthermore, in the HLbyL case, Cauchy’s integral theorem is unavailing. Contributions of order (απ)3 became relevant at the last BNL experiment:27 the remarkable accuracy of the aμ measurement indicated a deviation from theoretical predictions.28 Theorists proposed several model estimates of the aμ(HLbyL) contribution, which all agreed within the quoted errors. They found that the contribution came with an overall negative sign. Soon after the publication of the BNL result, this theoretical conclusion was questioned.29 There is a QCD limit at which the aμ(HLbyL) contribution is calculable. It is obtained in a model where the number of quark colors and the mass gap are allowed to increase without limit.30 In that unphysical limit, the contribution to aμ(LbyLS) turns out to be positive, implying that model calculations compatible with QCD must also give a positive result when model parameters are extrapolated accordingly. They all failed the test! The authors eventually found a convention inconsistency in their calculations which, when corrected, indeed gave a positive contribution. The significant discrepancy between theory and experiment was, if not eliminated, then reduced.
Conflicting theoretical estimates of aμ(LbyLS) created some confusion. At a workshop at the University of Glasgow in 2009, Lee Roberts suggested that three theorists of different groups get together and examine the discrepancies between models. He appointed Joachim Prades, Arkady Vainshtein, and me to do the job. Our result was aμ(LbyLS – Glasgow) = (10.5 ± 2.6) × 10–10, the so-called Glasgow consensus.31 There have been many evaluations of the aμ(LbyLS) contribution since then, using ever more sophisticated models. They turn out to be consistent, within errors, with the Glasgow consensus.
The evaluation of the aμ(LbyLS) contribution has also been undertaken by various LQCD collaborations. These are QCD first principle, model-independent evaluations, which little by little have reached a better level of accuracy than the Glasgow consensus.32 For all that, no one believes that the aμ(LbyLS) contribution can by itself explain the tension between theory and experiment.
Present Status of the Theoretical Contributions
The following table summarizes the status of the various theoretical contributions to the muon anomaly in 10–11units and prior to the FNAL result. Several comments are in order:
- The results in the third column of Table 1 show the level at which each contribution is effective.
- The aμ(QED) results from the interactions of photons and leptons include the contributions from the calculated coefficients of the first five powers in απ. The result in the first line has been evaluated using the value of the fine-structure constant α determined from a cesium atom interferometry experiment:33
α–1(Cs) = 137.035999046(27). - The entry in the second line of the table makes use of the high-precision determination of the electron g – 2 by Gerald Gabrielse’s group at Harvard,34
ae(exp.) = 1,159,652,180.73(28) × 10–12.
yielding
α–1(ae) = 137.0359991496(13)(14)(330).
The uncertainty of ±330 results from the error in the experimental determination of ae, ±14 from the hadronic contribution to ae and ±13 from the numerical evaluation of the (απ)5 QED term.35
One can conclude from these results that the theoretical contribution from the QED interactions of photons and leptons to the muon g – 2 is well known. - By aμ(HVP)lowest order, one means the HVP contribution from the Feynman graph in Figure 2. The third and fourth lines of Table 1 are the result of adding the third and fourth leading-order hadronic contributions. These results have been obtained using the dispersive HVP evaluation method described above near Figure 2.
- The contribution aμ(EW) from the electroweak interactions of the Standard Model is small because it is proportional to GFm2μ, where GF ~ 10–5 GeV–2 is the Fermi coupling constant that governs the strength of the weak interactions. Its evaluation is well understood in the Standard Model.36
Table 1.
| Contribution | Comments | Results |
|---|---|---|
| aμ(QED) | Photons and leptons, with α(Cs) | 116,584,718.931(30) |
| aμ(QED) | Photons and leptons, with α(ae) | 116,584,718.842(34) |
| aμ(HVP)lowest order | Experimental dispersive evaluations | 6,931(40) |
| aμ(HVP)total | Experimental dispersive evaluations | 6,845(40) |
| aμ(EW) | W±, Z0, and Higgs with leptons and quarks | 153.6(1.0) |
| aμ(HLbyL)total | Phenomenology and LQCD | 92(18) |
Theoretical contributions to the muon anomaly in units of 10–11.
The sum of the contributions listed in the results column of Table 1 gives
aμ(Th.WP) = 116,591,810(43) × 10–11,
which is the consensus reported in the 2020 white paper (WP).37 When compared to the experimental result aμ(2021) = 116,592,040(41) × 10–11 (0.35 ppm), the result indicates a significant 4.2σ difference—triggering in the literature, of course, speculations about whether new physics might be at work. Do notice that a discrepancy of 4.2σ is about twice the size of the electroweak contribution. The order of magnitude of what might be the contribution of new physics (NP) to the muon anomaly is expected to be: aμ(NP)∼aμ(EW)×(MWMNP)2× couplings with MNP≫MW. This would require that the couplings be fine tuned.
Many NP models have been excluded for that reason.
The situation is confusing. The same day that the results of the FNAL muon g – 2 collaboration were published,38 Nature published a new result by the Budapest–Marseille–Wuppertal (BMW) LQCD collaboration. At issue was the lowest-order HVP contribution to the muon g – 2. The result:39
aμ(HVP)BMW = 7,075(55) × 10–11,
which reduces the total discrepancy in aμ(2021) = 116,592,061(41) × 10–11 (0.35 ppm) from 4.2σ to 1.6σ.
The discrepancy is still there, but it is not significant enough to suggest that new physics is at work.
The BMW result is under detailed examination by other LQCD collaborations. They are expected to produce their own results. If the disagreement between LQCD and the experimental dispersive evaluation of the HVP persists, researchers will have to find the explanation for that. Because they involve integrals of different quantities, comparison of the two methods is difficult but not impossible.
As new statistics accumulate, the FNAL muon g – 2 experiment is expected to reduce their error. There is also a new experiment at the Japan Proton Accelerator Research Complex in Tokai. This J-PARC experiment E34 will employ a new and different technique to measure the muon anomaly.40 All this gives more time for the theorists to check and improve their calculations before the next awaited confrontation.