As the Loom of Physics Expands

This is the second in a series of essays. The first offered an historical appraisal of the elements of matter. The third will address the Standard Model.

Democritus, Epicurus, and Xenocrates regarded sound as a stream of particles.¹ Aristotle came closer to the truth:

Sound is composed of particular beating vibrations … created in the air by the body that gave out the tone … This motion propagates itself unchanged [as] each portion of the air sets the next portion of air in motion with the same movement as it has itself.²

Galileo Galilei and Isaac Newton, like Aristotle, favored waves, Newton deducing a simple formula for the speed of sound through a gas,

$\sqrt{\frac{p}{\rho }}$,

where p is the pressure of the gas and ρ is its density. In the case of sound traveling through air, his result was significantly in error. Newton invoked two quite absurd fudge factors to force his predictions to coincide with reality.³ The triumph of the wave theory of sound would have been unalloyed had not quantum mechanics blurred the distinction between particles and waves. And indeed sound in elastic solids often displays particle-like behavior. The particle avatars of sound were termed phonons in 1932, just six years after photons received their name.

Both Democritus and Aristotle regarded light as a stream of particles. Lucretius agreed:

The light and heat of the sun: these are composed of minute atoms which, when they are shoved off, lose no time in shooting across the interspace of air in the direction imparted by the shove.⁴

The Greeks found the law of reflection and sought a similar law for refraction. In 984 CE, Ibn Sahl found an empirical formula for refraction, but it was soon forgotten—like snow upon the desert’s dusty face, as a Persian mathematician remarked. The law was rediscovered by Willebrord Snellius (Snell) in the seventeenth century. In the version of Snell’s law worked out by René Descartes, light travels more slowly through air than water or glass; in Pierre de Fermat’s version, faster.

Newton deduced Snell’s law by inventing a short-range attractive force that would act between particles of light and matter.⁵ His imagined new force gave an impetus to photons just as they entered a denser medium, thereby increasing their speed and changing their direction in accord with Snell’s law. Ingenious! Note the curiously indirect way Newton presented his ideas:

These attractions bear a great resemblance to the reflexions and refractions of light … as was discovered by Snellius and Des Cartes … For it is now certain that light requires about 7 or 8 minutes to travel from the sun to the earth. Moreover, rays of light … as lately was discovered by Grimaldus … passing through a small hole are bent or refracted around these bodies as if they were attracted to them … Therefore I thought it not amiss to add the following Propositions for optical use; not at all considering the nature of the rays of light, or inquiring whether they are bodies or not.⁶

Here Newton alludes to two recent developments. In 1676, Ole Rømer had proven that light travels at a finite speed, using his observations of the varying eclipse intervals of Jupiter’s innermost moon Io to find a rough measure of its speed. Shortly before this, Francesco Grimaldi had found that light passing through a tiny aperture emerges as a cone. Light propagates and spreads “not only directly, and by refraction and reflexion,” he wrote, but also by a fourth mode, dubbing the phenomenon diffraction and recognizing it as a property shared by sound waves.⁷ Grimaldi’s discovery was a vital step toward Christiaan Huygens’ development of the wave theory of light. In this passage, Newton cites Grimaldi, misinterpreting diffraction as evidence for the bending of light particles by his conjectured force.⁸

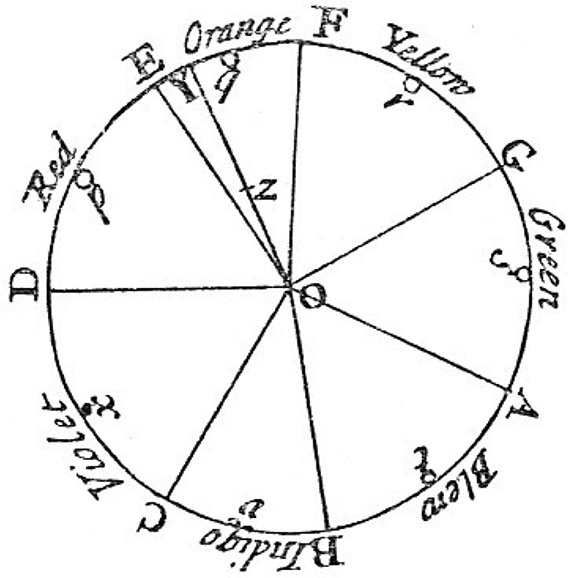
Much of Newton’s treatise on optics concerns his observations of the colored rings that appear when a thin lens is placed atop a glass plate.⁹ Newton called these phenomena “fits of easy transmission or reflection,” but his own data showed that the wavelengths associated with light span a factor of about two, or an octave, as he illustrated with a circular chart of seven colors divided by the seven notes of a diatonic musical scale. The intervals between E and F (orange), and B and C (indigo) are half the size of the other five, in accord with a piano’s tuning. Hence Newton chose seven colors for the rainbow.

In 1678, Huygens developed a wave theory of light from which Snell’s law followed. Huygens showed why light ordinarily travels in straight lines, but he could not explain diffraction. Early in the nineteenth century, Huygens’s wave theory was improved by Thomas Young in Britain and Augustin-Jean Fresnel in France. Superposition and interference of waves offered simple explanations for Newton’s rings and diffraction. Fresnel predicted that a bright spot would appear at the center of the shadow of an opaque disc, which seemed absurd, but in 1819 the remarkable scientist-adventurer-politician François Arago managed to spot the spot; his colleagues were flabbergasted.

Arago’s spot proved that light is comprised of waves, but the crucial experiment would involve a comparison between light’s speed in air and water. Arago designed a technique to do this, but failing eyesight forced him to assign the task to two younger colleagues, Hippolyte Fizeau and Léon Foucault. Collaborators at the start, they soon became fierce competitors. Each set out to measure the speed of light in air and to compare that to its speed in water. In 1849, Fizeau measured the speed of light to within five percent of its correct value. Soon afterward, both found that light travels more slowly in water than air, refuting both Newton and Descartes and confirming Huygens’s wave theory of light.

Electromagnetism

Newton’s theory of gravity required action at a distance. No one in the seventeenth century found this a particularly compelling idea, and neither did Newton.

That one body may act upon another at a distance through a vacuum, without the mediation of anything else … is to me so great an absurdity that I believe no man who has in philosophical matters a competent faculty of thinking can ever fall into it. Gravity must be caused by an agent … but whether this agent be material or immaterial, I have left open to the consideration of my readers.¹⁰

The same problem pertains to electric and magnetic forces. Michael Faraday introduced lines of force into the discussion, but these magnetic field lines were important only because they represented the first step in the elaboration of the concept of a field itself. There are today electric, magnetic, and gravitational fields. Defined at all points of space-time, they represent the potentiality of force. Newton’s agent, the gravitational field, is generated by mass. An electric charge produces an electric field everywhere, which exerts forces on other charges. Electric currents, which are charges in motion, produce magnetic fields, which exert forces on other moving charges.¹¹

James Clerk Maxwell, in his 1873 treatise A Dynamical Theory of the Electromagnetic Field, created a unified theory of electrical and magnetic phenomena: the discipline now known as electromagnetism or classical electrodynamics. A simplified version of his equations appears on the t-shirts of many physics students.¹²

∇ ⋅ E = ρ
∇ ⋅ B = 0
∇ × E = –Ḃ
∇ × B = Ė + J

What an achievement in concision these equations represent! They embody the results achieved by André-Marie Ampère, Charles-Augustin de Coulomb, Carl Friedrich Gauss, and Hans Christian Ørsted, amongst others. Physicists before Maxwell had understood much of the import of these equations, but it is the inconspicuous term Ė, appearing in the fourth equation, that is brand new. Maxwell needed Ė to make his equations consistent, but as so often happens in the history of physics, consistency enforces amazing and unexpected consequences. Maxwell’s equations give rise to solutions that are self-propagating oscillations of transverse electric and magnetic fields. These electromagnetic waves travel at the speed of light. Light is the visible portion of the vast electromagnetic spectrum.

Waves are disturbances that propagate through a medium. Such is the counsel of common sense. If this is so, how does light traverse the vacuum of outer space? Surely something must be there. For Maxwell that something was the luminiferous ether, a massless, intangible, invisible, and all-pervasive material, one possessing electromagnetic attributes but no mechanical properties.

The existence of Maxwell’s ether should have been easy to establish. His equations determine the speed of light relative to the ether. Hurtling around the sun, the earth must experience an intense ether wind. Light should appear faster or slower when measured with or against this wind. In 1887, Albert Michelson and Edward Morley set out to measure the predicted speed difference. No difference! They had glimpsed, but not recognized, the principle that would lead Albert Einstein to his theory of special relativity. The speed of light in a vacuum is the same to all uniformly moving observers. The speed of light is a universal constant denoted by c. The luminiferous ether has joined such discarded fancies as caloric, phlogiston, and vitalism. Light needs no medium. The changing electric field of a propagating light signal generates a magnetic field ahead of it, which in turn generates an electric field further along the light beam.

For electromagnetic radiation, the message itself serves as its own medium of transmission.

Waves are Particles

An ideal blackbody absorbs all incoming radiation and emits thermal radiation characteristic of its temperature. Nineteenth-century physicists found the laws to quantify the facts. The mean frequency of blackbody radiation is proportional to the Kelvin temperature of the body; its radiated power is proportional to the fourth power of its absolute temperature. Astronomers delighted in these results. Stars are blackbodies of a sort; their colors reveal their surface temperatures and luminosities.

Blackbody radiation challenged nineteenth-century physicists. No one could deduce a formula for the intensity and frequency distribution in terms of its temperature. In 1900, Max Planck introduced the radical hypothesis that light can only be emitted or absorbed in discrete and indivisible bundles that he termed quanta. The energy E carried by each light quantum is proportional to its frequency—E = hf, where Planck’s constant h, is a fundamental constant of nature, like c or the electron’s charge e.

Planck’s constant had no basis in classical physics. What meaning could there be to a quantized bundle of light waves? Still, Planck succeeded in deducing the formula for blackbody radiation. Five years later, Einstein fleshed out Planck’s hypothesis by attributing particle-like properties to light waves. “We are faced with a new kind of difficulty,” Einstein admitted. “We have two contradictory pictures of reality.” Light is both a particle and a wave. “[S]eparately neither of them fully explains the phenomena of light, but together they do!”¹³ Planck’s quanta and Einstein’s wave-particle duality initiated the quantum revolution.

Hydrogen is the most abundant element, its atom the lightest and simplest. Johann Balmer, in 1885, found its five visible spectral lines to satisfy a simple arithmetical rule.¹⁴ Was it mere coincidence, or did the rule conceal a profound truth? A decade later, Edward Pickering found a series of perplexing lines between those of hydrogen, but only in the spectra of very hot stars. Niels Bohr and his quantum rules would eventually explain both Pickering’s lines and Balmer’s formula.

Another puzzle of nineteenth-century physics began to emerge in 1839 when the team of Antoine and Edmond Becquerel discovered the photovoltaic effect, by which light produces electrical currents.¹⁵ The closely related photoelectric effect is the emission of electrons when ultraviolet light strikes a metal. Although the number of ejected electrons increases with the intensity of the light, Philipp Lenard found that the energy of those electrons increases with the frequency instead. At frequencies below a critical value no electrons are liberated, no matter how intense the light. In fact, the photoelectric effect cannot be explained in terms of light as electromagnetic waves.¹⁶ Einstein offered a radical explanation for the photoelectric effect:

The wave theory of light … has worked well in the representation of purely optical phenomena and will probably never be replaced by another theory … [but] phenomena connected with the emission or absorption of light are more readily understood if one assumes that the energy of light is discontinuously distributed in space … [T]he energy of a light ray … consists of a finite number of energy quanta which are localized in space, which move without dividing, and which can only be produced or absorbed as complete units.¹⁷

In the photoelectric process, as Einstein imagined it, each photoelectron is liberated by a single photon, its energy being that of the photon minus the energy needed to eject the electron. Einstein’s explanation was supported by Robert Millikan’s 1914 experiments and even more strongly by those of Arthur Compton in 1923.

Inside Atoms

Ernest Rutherford is among the few scientists who made their most famous discoveries after becoming Nobel laureates. Rutherford’s assistants in Manchester directed a beam of alpha particles from a radioactive source toward a thin gold foil target. They meant to measure small deflections of these particles upon striking gold atoms. Instead, the alpha particles were often deflected by large angles, sometimes even bouncing backward. “It was almost as incredible,” Rutherford recalled, “as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you … It was then I had the idea of an atom with a minute massive centre carrying a charge.”¹⁸ The result could only be understood if most of the atom’s mass is confined within a tiny nucleus.

Rutherford proposed that atoms are miniature solar systems, with electrons orbiting nuclei just as planets orbit the sun, and electrical forces playing the role of gravity. The hydrogen atom would then consist of a single electron orbiting a much heavier positively charged proton. This view faced an intractable problem. Maxwell’s laws require light to be emitted whenever electric charges accelerate. Orbiting electrons must accelerate toward their nuclei, and thus must emit light, lose energy, and spiral inward. Yet most atoms are perfectly stable. Classical physics offered no solution.

Bohr would find one.

Bohr earned his doctorate in 1911 then spent a year in England studying, researching, and visiting laboratories; in Manchester, he was received warmly by Rutherford. The following year Bohr returned to Copenhagen, and in 1913 he published three papers setting forth the first version of quantum theory. He began:

In order to explain the results of experiments on the scattering of α rays by matter, Prof. Rutherford has given a theory [in which atoms] consist of a positively charged nucleus surrounded by a system of electrons kept together by attractive forces from the nucleus; the total negative charge of the electrons is equal to the positive charge of the nucleus. Further, the nucleus is assumed to be the seat of the … mass of the atom, and to have linear dimensions exceedingly small compared with [those of] the whole atom.¹⁹

Bohr then pointed out how work on thermal radiation, the photoelectric effect, and X-rays indicate,

the inadequacy of the classical electrodynamics in describing the behavior of systems of atomic size. Whatever the alteration in the laws of motion of the electrons may be, it seems necessary to introduce … a quantity foreign to classical electrodynamics, i.e. Planck’s constant.²⁰

Bohr’s analysis assumed arbitrarily that only certain electronic orbits are permitted, each corresponding to a discrete stationary state of an atom. Upon emitting or absorbing a photon, an atom jumps from one stationary state to another, the photon carrying or supplying the energy difference between the two states. Atoms are ordinarily found in states of least energy, or ground states. Atoms are stable because no lower energy states exist.

Bohr went on to deduce the properties of atoms with just one orbital electron, such as hydrogen or singly ionized helium. Limiting himself to circular orbits, Bohr postulated “that the angular momentum of the electron round the nucleus in a stationary state of the system is equal to an entire multiple of a universal value.” This is a quantum constraint absent from classical physics, where angular momentum can assume any value at all.

Using Newtonian mechanics upon which he impressed a quantized angular momentum, Bohr calculated the allowed size and energy states of the hydrogen atom, determining its entire electromagnetic spectrum. He found not just the handful of visible lines satisfying Balmer’s formula, but all of its spectral lines, ranging from the infrared to the ultraviolet. “[T]here obviously can be no question,” Bohr wrote, “of a mechanical foundation of the calculations given in this paper.”²¹ Like Planck and Einstein, Bohr had moved beyond classical physics to express the first substantial intimations of quantum physics. He not only deduced the size and spectrum of hydrogen atoms, but found a truly satisfying solution to the mystery of Pickering’s lines: they were spectral lines of singly ionized helium, present only in the hottest stars. Einstein was delighted by this result.

A cardinal attribute of the emerging theory was first recognized by the French physicist Louis de Broglie:

After long reflection in solitude and meditation, I suddenly had the idea, during the year 1923, that the discovery made by Einstein in 1905 should be generalized by extending it to all material particles and notably to electrons.²²

There we have it. Light’s baffling wave-particle duality is shared by matter. Electrons, as well as atoms and other particles, can display wavelike properties, just as light waves can act as particles. The wavelength associated with a body with momentum p is simply h/p, just as it is for a photon. De Broglie’s intuition was confirmed in 1927, when electrons scattering from a crystal formed diffraction patterns identical to those made by X-rays with the same momentum as the electrons. The first electron microscopes were designed and built just four years later.

Particles and waves emerge from everyday life. Pebbles thrown into a lake are undeniably particles; their ripples are waves. But atoms do not respect our feelings about how things should be, nor does our language have words adequate to describe the microworld. Because Planck’s constant is so small, and things like baseballs, bees, and bacteria are so large, they are not noticeably affected by quantum mechanics. Relativistic effects like time dilation and length contraction are irrelevant to our daily lives, because the speed of light is a million times that of sound. Classical theories of mechanics and electromagnetism will never be discarded. Within their envelope of validity, they are absolutely true.

In 1925, Werner Heisenberg formulated his uncertainty principle. The order in which measurements are made matters. It is not possible to measure precisely the position and velocity of a particle at the same time; measurement of one necessarily disturbs a subsequent measurement of the other. The uncertainty principle reflects the noncommutativity of the operators linked to momentum and position. This result encapsulates the essential difference between classical and quantum theories.

To formulate a theory incorporating the uncertainty principle, Heisenberg, Max Born, and Pascual Jordan identified Bohr’s quantum states as vectors in a Hilbert space. Heisenberg identified quantum states as infinite-rank matrices acting on these state vectors. Shortly afterward, Erwin Schrödinger took a different tack, seeking a wave equation akin to those for sound and light, in order to describe de Broglie’s matter waves. Measurements were linked to noncommutative differential operators acting on a space-time-dependent wave function—now famous as the ψ function. It was Born who completed the new theory’s arch by providing a probabilistic interpretation of the wave function. The Jordan–Heisenberg and Schrödinger formulations of quantum mechanics were soon recognized as two formulations of the same theory.²³

Quantum mechanics not only tells us why copper is red, diamonds are hard, and rubber is stretchy, it underlies all of chemistry and biology. It is a theory of almost everything, except for gravity and nuclear phenomena.

From Dante Onward

In the sixteenth century, Nicolaus Copernicus put the sun at the center of the universe, just as Aristarchus of Samos had done two millennia before. Neither theory was widely accepted. And for obvious reasons. Anyone on a speeding planet, common sense might suggest, would be aware of its motion.

In Inferno, Dante Alighieri described the descent from the seventh to the eighth circle of the underworld. He is flying atop the infernal monster Geryon.

Than was my own, when I perceived myself
on all sides in the air, and saw extinguished
the sight of everything but of the monster.
Onward he goeth, swimming slowly, slowly;
Wheels and descends, but I perceive it only
by wind upon my face and from below.²⁴

Dante’s wildly imagined flight, as Leonardo Ricci realized, “captures a physical law of motion”:

[Dante] is not aware (or, more accurately, he imagines that he is not aware) of anything but the apparent wind. He asserts that, aside from the effect of the wind, his sensation of flying is not dissimilar to being at rest … Dante intuitively grasped the concept [now known as Galilean invariance], but unlike Galileo, he did not pursue this idea any further.²⁵

Three centuries later, Galileo proffered his own thought experiment, showing that one’s uniform motion cannot be detected:

Shut yourself up with some friend … below decks on some large ship, and have with you there some flies, butterflies, and other small flying animals. Have a large bowl of water with some fish in it; hang up a bottle that empties drop by drop into a wide vessel beneath it. With the ship standing still, observe carefully how the little animals fly with equal speed to all sides of the cabin. The fish swim indifferently in all directions; the drops fall into the vessel beneath; and, in throwing something to your friend, you need throw it no more strongly in one direction than another … When you have observed all these things carefully … have the ship proceed with any speed you like, so long as the motion is uniform and not fluctuating this way and that. You will discover not the least change in all the effects named, nor could you tell from any of them whether the ship was moving or standing still … The cause of all these correspondences of effects is the fact that the ship’s motion is common to all the things contained in it, and to the air also.²⁶

Galileo never precisely enunciated his principle of invariance; he was besotted with circular motion, not unbounded rectilinear motion. Nor, for the same reason, did he accept Johannes Kepler’s planetary ellipses.

The principle may have been first stated by Descartes in 1644, two years after Galileo’s death and Newton’s birth: “Each and every thing, insofar as it can, always continues in its same state,” and, “all motion is, of itself, along straight lines.”²⁷ The principle reappeared in Newton’s Principia Mathematica, rather more clearly stated, and credited to Galileo as the first of his three laws of motion: “Every body continues in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed upon it.”²⁸ Whether due to Galileo, Descartes, or Newton, this law underlies the notion of Galilean invariance. The laws of physics are the same to all uniformly moving or inertial observers, whether they are on the earth, or the International Space Station, or on a planet receding from the earth at half the speed of light.²⁹

Newton’s second and third laws of motion are the foundations of classical mechanics. His second law offers a definition of force as the product of mass and acceleration. His third law, that every action is accompanied by an equal and opposite reaction, is equivalent to the law of the conservation of momentum. Newton invented the calculus, which he called the method of fluxions, and used it to calculate planetary orbits, thereby initiating the science of celestial mechanics, but his most profound insight was expressed by the law of universal gravitational attraction. All objects in the universe attract one another with a force that is proportional to their mass and inversely proportional to the square of the distance between them. No one had before seen this. Together with his laws of motion, Newton’s law of gravitational attraction allowed him to create a unified theory of motion on earth and in the heavens.³⁰

Daniel Bernoulli, Coulomb, and Joseph-Louis Lagrange all made their careers by developing and exploiting Newtonian mechanics. But the most dramatic scientific event of the eighteenth century had little to do with Newtonian mechanics per se: the 1781 discovery of the seventh planet, Uranus, by William Herschel. Its orbital radius accidentally agreed with the empirical Titius–Bode law, but that now-discarded bit of numerology did inspire astronomers to discover the largest asteroids: Ceres (1801), Pallas (1802), Juno (1804), and Vesta (1807), all of them moving in accordance with Newton’s laws.

As astronomical measurements became more precise, an anomaly was found in the orbit of Uranus. John Couch Adams and Urbain Le Verrier independently showed that the effects of an eighth planet lying beyond Uranus could explain the discrepancy. They computed its mass and orbit, enabling Johann Galle to find the new planet in 1846.³¹

The anomalous behavior of Mercury represented another challenge to Newton’s theory. Le Verrier found the rate of precession of its orbit to exceed what could be accounted for by the gravitational effects of other planets. He attributed the discrepancy—a mere forty-two arc seconds per century—to the gravitational effects of a new planet with a smaller orbit. He named it Vulcan and announced its discovery to the Académie des Sciences in 1860. Le Verrier died in 1877, still believing that he had discovered both Neptune and Vulcan. Astronomers would have to wait until 1916 for Einstein to solve the problem of Mercury’s orbital anomaly with his new and improved theory of gravity: the general theory of relativity.

The Special Theory of Relativity

Many nineteenth-century issues led Einstein toward special relativity. Fizeau was one of the first to show that light travels more slowly in water than in air. In 1851, he measured the difference in speed between light traveling with moving water and light traveling against it. If Maxwell’s luminiferous ether was unaffected by water, there should be no difference in speed; if it were it dragged along by the water, the difference should be twice the speed of the water. Fizeau obtained a mystifying result that lay between these plausible extremes. Equally relevant was the negative result of the Michelson–Morley experiment.

Einstein presented his special theory of relativity in a 1905 paper entitled “On the Electrodynamics of Moving Bodies”:

Examples of this sort, together with the unsuccessful attempts to discover any motion of the earth relatively to the “light medium” suggest that the phenomena of electrodynamics as well as mechanics possess no properties corresponding to the idea of absolute rest. They suggest rather that … the same laws of electrodynamics and optics will be valid for all frames of reference for which the equations of mechanics hold good. We will raise this conjecture … to the status of a postulate, and also introduce another postulate, which is only apparently irreconcilable with the former, namely, that light is always propagated in empty space with a definite velocity c which is independent of the state of motion of the emitting body. These two postulates suffice for the attainment of a simple and consistent theory of the electrodynamics for moving bodies based on Maxwell’s theory for stationary bodies. The introduction of a “luminiferous æther” will prove to be superfluous inasmuch as the view here to be developed will not require an “absolutely stationary space” provided with special properties…³²

Einstein’s second postulate—that the speed of light is the same relative to all observers whatever their state of motion—is certainly counterintuitive. Its consequences are even stranger. Why can neither mass nor message travel faster than light?³³ How can events be simultaneous to one observer, but not to another? Why do the lengths of rulers or the rates of clocks differ for observers in different inertial systems?

The answers are tied to another and more fundamental question: which space-time quantities are the same when measured by any inertial observer? Let two events be designated as (x₁, t₁) and (x₂, t₂), where vectors x_i denote their positions and t_i their times. Classical mechanics admits two space-time invariants, quantities that are the same to all inertial observers: the distance, and time interval between the events, d = |x₂ – x₁| and τ = t₂ – t₁. The Galilean transformations of classical mechanics are those linear transformations of space and time that leave both d and τ unchanged. The relevant Galilean transformation is x′ = x – vt, and t′ = t. In special relativity the sole space-time invariant is the combination d² – τ². Lorentz transformations are those linear transformations that leave it unchanged: x′ = x cosh φ – ct sinh φ, and ct′ = ct cosh φ + x sinh φ, with v ≡ c tanh φ. These formulas approach the corresponding Galilean formulas in the limit of small v. A sequence of two Lorentz transformations by speeds v = c tanh φ and u = c tanh ψ in the same direction results in the Lorentz transformation corresponding to the speed w = c tanh (φ + ψ), where

$w=\frac{u + v}{1 + uv / c^2}.$

This is the relativistic law for the addition of velocities. For small u and v it approaches the familiar result u + v. It is the speed of a ball caught by a girl at rest, thrown at speed u by a boy running toward the girl at speed v. Otherwise, the law informs us that the composition of any two subluminal velocities is subluminal, and that the composition of c with any subluminal velocity remains c.

Special relativity also changes our understanding of momentum and energy, which are linked to one another, just as are position and time. The best known is Einstein’s deceptively simple formula E = mc², stating the equivalence of matter and energy.³⁴ It replaces the conservation laws for mass and for energy with a single law.

The General Theory of Relativity

Special Relativity is relevant only in uniformly moving reference frames. It cannot be used by accelerated observers. It was for this reason that it was called special. In 1907, Einstein had what he described as the happiest thought of his life:

[B]ecause for an observer falling freely … there exists … no gravitational field … [he] has the right to consider his state as “at rest.” … The experimentally known matter independence of the acceleration of fall [the equivalence principle] is therefore a powerful argument for the fact that the relativity postulate has to be extended to coordinate systems which, relative to each other, are in non-uniform motion.³⁵

Einstein realized that a person in a sealed elevator cannot tell gravity from acceleration. Gravitational forces are merely epiphenomenological consequences of the distortion of space-time produced by matter. A generally covariant theory is one whose physical laws are the same to all observers whatever their state of motion. Because gravitational forces and those experienced by accelerated observers are locally indistinguishable, such a theory would have to encompass gravity. Einstein succeeded in his ambitious quest in 1915, in the middle of the First World War.

Einstein’s theory has led us to quantitative theories of cosmology and cosmogenesis, toward an understanding of the history of the universe from the creation of the first atomic nuclei in the Hot Big Bang to the evolution of all the stars, galaxies and the wondrous large-scale structure of the universe. Months after Einstein completed his general theory, he proposed three classic tests.

The first of these was carried out well before Einstein’s birth. The observed precession of Mercury’s orbit could not be explained by the gravitational effects of the sun and the other planets. Le Verrier attributed this discrepancy to Vulcan. To Einstein’s delight, Mercury’s behavior accorded precisely with his new theory of gravity.

Newtonian physics predicts that starlight skimming the solar surface should be deflected by the tiny angle of 0.87 arc seconds.³⁶ Einstein published a similar result in 1911. His general theory of 1915 predicted twice as large a deflection. At the time, the deflection could only be observed during a total solar eclipse. The test would wait for the first such eclipse after the armistice, in 1919, when a British expedition led by Arthur Eddington traveled to Brazil to perform the observations. Their result was in rough agreement with Einstein’s theory.³⁷

Robert Pound and Glen Rebka performed Einstein’s third test in 1960. They showed that an atomic clock in the cellar of the Jefferson Laboratory ticked a bit more slowly than an identical clock in the attic. A closely related and so-called fourth test of general relativity was proposed by Irwin Shapiro in 1964.³⁸ He pointed out that a radar signal grazing the sun on a round-trip to a planet or satellite would suffer a gravitational time delay of about two hundred microseconds. The effect was soon observed; it would later enable the most sensitive tests of general relativity.